Page 19
~ The Study of Threes ~
http://threesology.org
| Hybrids page 1 | Hybrids page 2 | Hybrids page 3 | Hybrids page 4 | Hybrids page 5 |
| Hybrids page 6 | Hybrids page 7 | Hybrids page 8 | Hybrids page 9 | Hybrids page 10 |
| Hybrids page 11 | Hybrids page 12 Playmate God |
Hybrids 13 Economics 1 |
Hybrids 14 Economics 2 |
Hybrids 15 Economics 3 |
| Hybrids 16 Economics 4 |
Hybrids 17 Economics 5 |
Hybrids 18 Economics 6 |
Hybrids 19 Economics 7 |
Hybrids 20 Language 1 |
| Hybrids 21 Language 2 |
Hybrids 22 Language 3 |
Hybrids 23 Language 4 |
Hybrids 24 Physics |
Hybrids 25 |
| Hybrids 26 | Hybrid 27 |
Visitors as of 30th July, 2021

Again we must ask ourselves to step back and review the question of what is most important to be studied as a basic construct of fundamental ideas to be discovered and discussed concerning the hybridizations found in Economics. Commonly, some readers look to mathematics to provide the scaffolding for blue-printing the foundational architecture of conceptualizations regardless of subject. Many people think that anything and everything can be reduced to number, while at the same time overlook the over-riding presence of two-patterned orientations in mathematics as I attempt to convey on this page: Simplistic Dualities and Mathematics page 3.
Here is a sampling of patterns-of-two in mathematics:
- Add and Subtract
- Multiply and Divide
- Rational numbers/Irrational numbers
- Two sides of an equation
- Fractions/Whole Numbers
- Greater than/ Less than
- Greater than or Equal to
- Less than or Equal to
- Valid equation/False equation
- lower numbers/higher numbers
- Positive/Negative (adding "neutral" makes it a pattern-of-three)
- etc...
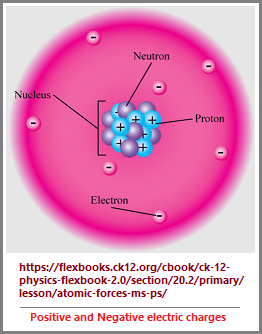
Yes, I know there are other basic patterns, but how often do you encounter such patterns being examined among different disciplines, making note of the recurrence of a conservation, despite the fact we have an infinity of numbers? Human conceptualization is stuck in a double-entry accounting profile, though those who are more "self" oriented may use a single entry formula. Whereas Europeans developed one for commercialized goods and services, the Chinese tried to devise one for all of Nature called the Yin and Yang ideology. In Biology we see one called the Binomial Nomenclature for their audit of different life forms. While some double-entry auditing lists contain multiple items, others are used to reference a single observance such as in the case of negative and positive electric charges of atomic particles.
In computing we see the use of an auditing system called Binary language. Religions routinely use the old double-entry accounting system of Heaven/Hell, While some systems are simplistic and appreciably out-dated, others give the impression of being progressively modernized even though such vocabulary as might be employed is nothing more than an attempt to camouflage an underlying simplistic pattern based on superstition which the so-called modern education systems of the world have done a poor job in eradicating for the benefit of humanity. With respect to the heaven/hell dichotomy, it should be referenced herein as an above and below pattern so as to distinguish the existence of a basic formula and not as a means by which labels can be attached and used to support one or another religious doctrine. The good versus bad dichotomy shows up in various conceptual models such as for example, whether one views a two-tier business model from an ownership and managerial perspective or an employee perspective where a "two-tier" model might be to pay experienced employees a different wage and benefit package than new, inexperienced employees.
Clearly, the hot/cold, wet/dry, stormy/calm, etc... climates of Earth along with the bipedal (pendulum) influences of the human gait have contributed to a retention of the old double-entry cognitive pattern seen in religions, politics (such as political factions), fashion, dance, sexual orientation (the "Pride" community is even more primitive with its advocacy of single entry accounting), and multiple other human activities. Nonetheless, though most people take opposites or patterns-of-two for granted, and one can surmise that individual perception can determine the definition of what is meant by opposition, let us attempt to conjecture the existence of a finite quantity of the "two", irrespective of the labeling one might select to appropriate as the preferred vernacular, in that there is a lingua franca of kinds one might be able to deduce. For example, we have the oppositional form of the "two" as expressed by the Yin/Yang profile. We also have the series type of two such as in the case of a one- two progression, though we might wrestle for a time with the two-pattern represented in the fashion of a direct current example with its direct positive and negative orientations. With this in mind we come to a "two" in which a type of reversal appears that we might denote as Alternating current. From these observations one might step in the direction of allocating to our collection of twos, the item we call parallel, or a side-by-side pattern-of-two. And if we think about an inter-dimensional linkage, it is not certain whether we have actually found a different type of "two-pattern" or just an elaboration of one or another already cited in our three-dimensional perspective. By extension, if we view the "two" in relation to the three movements one might use when changing the direction of a chess piece, can we thus define the "two" in terms of a horizontal, vertical and diagonal frame of reference which then details three different possible types or kinds of the "two"? Previously, I portrayed three kinds of "twos" which were more than mere language (vernacular) or symbol swaps:

The same inclination to overlook the large presence of dichotomies in mathematics is occurring with those interested in Economics. Again and again and again there is a usage of various patterns-of-two yet few are publicly acknowledging such a usage as a recurring cognitive theme that should be addressed suspiciously, instead of using the recurring usage of dichotomies and other patterns-of-two profiles found in mathematics as a support feature which provides evidence for some presumed superiority or uniqueness by way of an association thereto as a reversal of the idea about someone or something being guilty by association; whereby to be associated with mathematics is not to be found only innocent but somehow be amalgamated with some preeminence of thought processing and overall definitively grand stature. Whereas it is difficult for those who are unacknowledgly accustomed to using dichotomies and other types of patterns-of-twos to formulate and express their ideas, an effort is being made to increase their panoramic and peripheral visions into a trinocular orientation and not simply a binocular perspective attached to a bipedal gait whose physiological reverberations have sprung into existence a cognitive preference for like-mindedness in speech patterns which set into practice a form of blindness (like horse blinders) whereby they trod the same path without the need of form reins of socialization and culturalization in their respective personal and professional climates, atmospheres and environments.
Whereas in several cases I have introduced the usage of patterns-of-three when entitling a page as being representative of dichotomies, my efforts at showing a contrast has sometimes been misinterpreted as illustrating information which appears to some as being "off-topic". However, with such a tool I have indeed been fortunate in poking the otherwise quiet two-patterned buzzings of the Economic's hive by stirring up the nest into realizing it honeycombs of idealization are not the only pattern which can be used for constructive purposes. Indeed, though some would argue that many components of our physiology are two-patterned constructed such as eyes, ears, hands, feet, testicles, jaws, nostrils, etc., they fail to consider that the usage of the two eyes contains three color cones, that the two ears have three bones and that the presence of three semi-circular canals produces a gyroscopic-like means by which the two legs and arms swinging in a pendulum rhythm are given balance. No less, it is of need for some Economists to take into consideration a List of threes in anatomy as compiled by Dr. McNulty and his associates.
Whereas we may claim there are different representative types of a given pattern, take for example the word "two", we might use two lines, dots or some other geometric form of "doodle". Likewise with the usage of words such as two, twice, double, etc... We may claim one style as an opposite and another as a reverse, while another is parallel and another as a sequence. Whereas we say one example is a parallel, is this not also a sequence since one item must follow another in the effort of one's expression regardless of how they may be placed? Hence, is the series model a fundamental pattern and others are hybrids? While a series may not also express opposition, neither does it express a reversal. Whereas the Yin/Yang profile expresses opposition though some prefer to see a complement, the Janus figure can be seen to express a serial, a reversal and an opposite... depending on one's preference of observation. Since we do not place two numbers at the same time, the act of one coming after another is a serial activity.
A study of Economics warrants a broader study of human behavior that is influenced by different factors such as both the internal (physical/nutritional) and external (planetary) environments. In looking at different subjects one finds basic patterns and those patterns are frequently reduced to enumeration. However, in studying enumeration in the context of mathematics, we find that it too has basic patterns which re-occur with a frequency that needs to be analyzed in a broader context since mathematics, like all subjects, are made-up constructs of the same human brain matter. Not necessarily the same mind, but the same basic biological 'stuff' that all of us have, albeit with different neuronal activity. Nonetheless, repeating patterns in the Stock Market may necessarily recur due to the usage of similar patterns being used in human thinking, despite what terminology may be employed from one era to the next. In addition, if the same basic patterns are recurring and there seems to be an unrecognized "deliberate" recurrence of some patterns over others, though the possibility of having as many as there are numbers might be a consideration; we are thus faced with the consideration that a force conservation in Economics thinking is taking place. We can not actually, really, truly come up with new ideas containing different patterns of conceptualization to effect advanced thinking in economics, because we are too consumed with the usage of coining different terms which conceal from us the occurrence of the same basic patterns being forced upon us to be used as a survival mechanism due to an incrementally deteriorating planetary and solar system environment which requires the usage of a conservation of repetition as a survival mechanism.
The repetitious usage of pattern-of-two ideas in Economics and other subjects is a tale-tell sign that humanity is being subjected to conditions which are forcing (enforcing) the usage of a small set of patterns just like there is (astonishingly) but a few elements in the whole of the Universe as seen from the vantage point of Earth. It is rather incredible that all of biology relies on a few recurring patterns one of which is a triplet code, though our numbering system is infinite. While some may claim this to be "God's" will, I would rather say that this is due to a forced conservation. Like wise in our perception of what constitute the three families of fundamental particles found in atomic physics. While some Economists are salivating and slobbering over a quick and short-term profit due to some idea they pursue by using the same underlying patterns with different words in different contexts to convince others they have developed a new insight, they are overlooking the long-term loss of the species due to unreplenishable resources whose incremental deteriorations affect the economic reality humanity has to cope with. In short, they are not looking at a larger picture but a selfie portrait in their pursuit of some applied idea to reap a profit from.
Let us take a look at mathematics as if we are attempting to analyze its historical development in connection with the development of Economics from its earliest beginnings as well, all the while keeping in mind that mathematics will later be used in different sectors of economics (such as the stock market), and that the history of Economics must be scrutinized as well with the intent of discerning basic patterns reduced to a number scheme. While Economics is frequently portrayed in what can be described as "pictographic" commentary such as the different commodities, some have chosen to move their discussions and interests towards a usage of what might be described as "higher economics" since mathematics too was once conversed about and displayed with pictographic conversations and illustrations. However, while some readers may easily discern the comparison without an elaboration, let me elaborate for those who have difficulty in recognizing the verbal and illustrated pictographs used by many economists who prefer this over the usage of a strict language usage involving numbers and symbols alone.
It is not too difficult for the reader to pick up a book on early mathematics to discover that early mathematics was generally concerned with basic arithmetic involving goods such as wheat, salt, animals, spices, etc... Symbols along with numbers may have been used, but the intent of such observations is to emphasize the development of mathematics and not the development of Economics as a brand or kind of thinking as well. While basic arithmetic often occurred hand in hand with economic concerns and considerations, both later diverged to become their own disciplines, though in many cases they shared a conjoined past. Both used the other as their preferred model of pictograph language, though it is infrequent for someone to encounter a writer describing mathematics as a form of pictograph illustration being used to supplement Economics. It is the reverse of this that is the typical presentation. That is, economic/commercial interests were the pictographs used to supplement an understanding of mathematics instead of mathematics being used as pictographs used to supplement an understanding of economic and commercial interests. In this perspective, one must ask which of the two is the more basic thinking pattern? Did a usage of some basic economic pattern come before a basic interest in numbers or counting?
If we say that the dichotomy of "give and take" (share and steal) preceded the conceptual development of plus and minus or gain and loss, then it may be necessary to conclude that enumeration and all of mathematics is an elaborated, is a hybridated model of more fundamental cognitive activity, even if the human brain uses such but is not necessarily conscious of its presence. For example, does other life forms develop an awareness of their survival efforts as expressions of an economics or mathematics consistent with the species in question? Does a horse think about economics and mathematics in horse terms and realizations, even if humans are oblivious to such mental contemplations on the part of a horse or other life form? By extension, does god know he, she or it is a god or are the supposed activities of a supposed god taking place on a level that a god does them by way of instincts, reflexes or other taken-for-granted activities without either being concerned with them or not taking the time to analyze them even though they are capable of doing so? Then also, let us consider the idea that both economics and mathematics are pictographs of other more fundamental brain activity humans have not as yet grown out of using.
"Correspondence Counting" is the phrase that has been used to describe the use of counting with everyday commodities such as jars, animals, loaves of bread and the like. Later on the objects could become pictographs that later became words and still later altered to symbols, though I do not say this is the sequence which actually took place. The point is to present the consideration that the idea of enumeration (for counting) and then arithmetic followed by geometry then mathematics may well be supplemental derivations of more fundamental brain processes indicated by simple economic expressions involving day to day commodities which could be used to develop a far more expansive intellectual activity if we would back track to the origin of the initial cognitive activity and redirect it along a different course whereby mathematics is more easily recognized as an offshoot of it which retains a primivity of design and usage that human brain activity has the capacity to move beyond. The contemplation of such a consideration should not lead one astray from recognizing that correspondence counting is another reference to paring and one-to-to association, otherwise noted as a pattern-of-two.

Clearly, correspondence counting has utility, but attempting to state correspondence counting in this sense as if it were a law, leads to the problem of inflexible thinking where a temperature of ten degrees and a temperature of twenty degrees placed together does not lead to a temperature of 30 degrees. Using conventional mathematics based on correspondence counting in a pragmatic or rural sense leads to the development of a mathematics with an inflexibility which does not allow for anyone to question mathematical reasoning to the extent that it can have hybridizations beyond the typical divisions such as geometry, arithmetic, Algebra and Calculus. While these are useful, they can lead one to think of them as "set in stone" or "Universal law" or "god given" factualities presenting some with the notion that Mathematics is Queen and no revolution in Mathematics is possible to dethrone the Monarchy and develop a better system of thinking than that being applied to everyday interests and taught in school as a requirement.
While some might want to say we have conventional mathematics, there also exists unconventional mathematics, without realizing they have created yet another example of a dichotomy and that such recurrences relate to a forced conservation due to humans having to correspond their ideas to a condition of incremental deterioration as an attempted survival mechanism. In most instances we may see mathematicians taking conventional mathematics and "tweaking" it to create an equation which will provide for the inclusion of material that was previously being used as an example of non-conventional mathematics, just like some Economist will take variables into consideration that were not done so in their initial development of a theory, in order to show that their theory does in fact or can be enlarged to incorporate such variables... thus trying to persuade nay-sayers that their idea was more comprehensive than they had fist considered. Instead of saying they were wrong, which might be used by an adversary to claim they could be wrong at a future occasion as well and should be replaced; the act of being honest must be tempered with an ability to incorporate adversarial components to the development of a new theory so long as they do not attempt it to be a means by which they can use it as a wedge to strengthen their own position. If one is to be honest, one must require all those involved in a transition towards the development of something new and bold to be just as honest and forthcoming by setting up publicly viewed parameters which would easily reveal any deception or ulterior motive.
If I may add another example of unconventional mathematics, the equation of 1 + 1 = 3 appears to be wrong, unless one is told that the numbers relate to a relate to a relationship between a man and woman having a child. It is not that conventional mathematics is wrong in this instance, it is that mathematics is being wrongly used. It does not adequately constitute the weight of an argument for either denying the validity of mathematics being used in a conventional way nor that mathematics is wrong and needs to be replaced. It simply illustrates humanity has not come to terms with the existence of an underlying model of conceptual processing that does not adequately lend itself to an accurate self-portrait by using any of the standardized convention conceptual orientations being used by any single subject occurring in the present era. In short, there is something (let us say conceptual or cognitive activity) which may be more fundamental... with a great developmental potential, then either mathematics or economics can portray. Bits and pieces of it may well be represented from time to time by those we might otherwise deem as insane, which is another label for unconventional. The phrase "super sanity" is sometimes use to denote those who have achieved some level of sobriety conventionally described as "seeing through the nonsense" or hypocrisy of everyday activities which occur in politics and social entanglements described by news-casters.
With respect to the present perspective, let me provide an example of those who are similarly oriented... to some degree, as I am trying to convey, but must note that the authors are not exactly describing "cognitive fundamentals", at least from an attempted historical approach that I am scratching the surface of:
1 + 1 = 3: Synergy Arithmetic in Economics
Mark Burgin and Gunter Meissner
UCLA Department of Mathematics, Marina Del Rey, USA.
University of Hawaii, Honolulu, USA.
DOI: 10.4236/am.2017.82011
Abstract
Counting has always been one of the most important operations for human be-ings. Naturally, it is inherent in economics and business. We count with the unique arithmetic, which humans have used for millennia. However, over time, the most inquisitive thinkers have questioned the validity of standard arithmetic in certain settings. It started in ancient Greece with the famous philosopher Zeno of Elea, who elaborated a number of paradoxes questioning popular knowledge. Millennia later, the famous German researcher Herman Helmholtz (1821-1894) expressed reservations about applicability of conventional arithmetic with respect to physical phenomena. In the 20th and 21st century, mathematicians such as Yesenin-Volpin (1960), Van Bendegem (1994), Rosinger (2008) and others articulated similar concerns. In validation, in the 20th century expressions such as 1 + 1 = 3 or 1 + 1 = 1 occurred to reflect important characteristics of economic, business, and social processes. We call these expressions synergy arithmetic. It is common notion that synergy arithmetic has no meaning mathematically. However in this paper we mathematically ground and explicate synergy arithmetic.
The authors in the above excerpt provide the following paradox as an example of the content they have generated:
...An example of this type of reasoning is the paradox of the heap (or the Sorites paradox where s???? is the Greek word for "heap"). It is possible to formulate this paradox in the following way:
1) One million grains of sand make a heap.
2) If one grain of sand is added to this heap, the heap stays the same.
3) However, when we add 1 to any natural number, we always get a new number.
While... yes, their representation is easily understood, they overlook the position of an observer who can just as easily call the new quantity a "heap", in keeping with the language of the context being illustratively described. A similar semantics issue arises when we speak of the development of quantity to numerical symbol alignment such as in the early history of counting there was (we assume) not only a symbol such as "1" (or a line or a notch) used for the quantity "one", and then a symbol such as "2" (or two notches) for the quantity "two"; though after the quantity of one there is thought to have been a delay in the development for the quantity "two" due to the need for developmental processing and creativity to mature. In such a case a word such as much or many or heap or whatever may have been used to describe all quantities beyond one. A word such as "heap" or "bunch" or "many" may or may not have been employed. Likewise a similar occurrence may have taken place when the "two" was cognitively reached. The next value for the quantity "three" may have garnered a usage for the same term once used for "two", whereby any quantity beyond two was viewed as a heap, or much, or many, or a bunch, or whatever term was common place or even prosaic at a given place and time. The word nonetheless stood as the place holder of the third position in the counting scheme, if one chooses to count in this fashion, even if it differs from the convention of usage commonly expressed by a given person, group of people, culture, or larger society. If I add 123 + 123 and claim it as 456 or 789, this may not be mathematically correct, but it is correct in terms of sequential thinking which is regarding the usage of numbers as corresponding connectives just as some psychiatric patients use clang associations. If one changes the numbers to words and the words to sounds which may or may not rhyme; this too is not mathematically correct in a given sense, but may nonetheless be revealing an underlying cognitive theme which predates the conceptualizations of both economics and mathematics just as babbling and pre-babbling utterances predate the usage of words. While we hear the sounds of babbling and pre-babbling, we do not understand them as basic cognitive patterns related to basic brain functioning that is learning to actively exercise in the manner consistent with the physiological tools which an infant is born with in the environment to which it is born and subjected to those who may or may not have an extensive knowledge except for those which a modern day person would describe as rudimentary or primitive, but are adequate within the context that the person using them finds application thereof.
Date of (series) Origination: Friday, 30th July, 2021... 6:38 AM
Date of (this page's) Initial Posting: Friday, 10th December, 2021... 6:45 PM