~ 1 ~
~ The Study of Threes ~
http://threesology.org
Researchers as of 8/29/2019
| Devil's Advocate Series: | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14A 14B |
15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22A 22B |
23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 A | 30 B | 31 | 32 | 33a | 33b | 33c |
| 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 A | 41 B |

In my effort to strive for objectiveness in my research efforts of the "threes" phenomena, I am forced into a present day variation of the old Devil's Advocate role. Let us begin this series with a short definition of "Devil's Advocate" culled from several sources, including the usage of the image as a link:
- Wikipedia: The Advocatus Diaboli (Latin for Devil's Advocate) is a former official position within the Catholic Church, the Promoter of the Faith: one who "argued against the canonization (sainthood) of a candidate in order to uncover any character flaws or misrepresentation of the evidence favoring canonization."
- Oxford Dictionary: A person who expresses a contentious opinion in order to provoke debate or test the strength of the opposing arguments.
- Collins Dictionary: If you play devil's advocate in a discussion or debate, you express an opinion which you may not agree with but which is very different to what other people have been saying, in order to make the argument more interesting.
- Business Dictionary: Person who identifies and challenges the flaws in an assessment, plan, or strategy.
- Forbes: The devil’s advocate is, if
you will, in the details. We’ve found that there are three keys to success:
- You have to commit to an explicit process rather than hope that tough questions will spontaneously emerge...
- The goal of devil’s advocacy must be framed correctly...
- The devil’s advocate needs to function constructively throughout the innovation process rather than be an inquisition at the end...
In my own self-appointed role as a Devil's advocate, I have found this position to be quite advantageous on several undivulged occasions that no doubt many of us use both consciously and unconsciously on one or another venture. As it is playing out, my former numerological interest in the "threes phenomena" is maturing along a path which many sciences have. I don't mind having played the role of an alchemist in the early stages, so long as it is eventually recognized that research interests and efforts can evolve, like Alchemy into Chemistry, Astrology into Astronomy, war exercises into sports exercises, nature relationship/worship to "natural law" advocacy, etc...
If one can imagine it, there is an ongoing timeline of timelines taking place, of which the following was constructed off the top of my head in a moment's sideline of musefulness to give but a handful of examples:

The usage of a timeline will serve the purpose of identifying not only the recurrence of three-patterned examples of development, but also where other-than-the-three pattern comes into play. If it is true, (and I will refer to this on other occasions as well that) as is suggested by the one-one-three development of the three Germ Layers which have developed along a:
..that this (1-2-3) sequencing is an underlying "law, rule, proclivity", etc..., of biology, then its presence or absence is signifying particular conditions within,(and/or) alongside, (and/or) outside a given activity. And it doesn't matter if one disagrees with the notion of a proclivity in terms of whether this or that cell(s) become endodermal, mesodermal or ectodermal... since the fact of the matter is there remains a recurring limitation to the quantity of overall steps. In other words, while some may argue for a quadroblastic Germ layer assortment, this too pays reference to the ongoing limitation. Pointedly stated, we are not seeing a five, six, seven.... 28... 149, etc... grouping. We pay witness to a low number situation which may itself be a tell-tale sign of an imposed restriction... though some might use a "nice word" such as conservation, thereby overlooking any possible predation that the environment is exercising against biological development.
As an interjected aside reference, it is of some interest to note that the notion of a "1-2-3 maturational development sequence"... and its divergent extrapolations (into the realm of "many", like an ancient system of counting), is recognized in many different "tongues" of communication (words, symbols, music, etc...) or otherwise known in the language respective of a given subject and context, one of which is philosophy. One which came to mind that I had come across years ago is credited to a person whom is called Laozi:
Laozi (author of Tao Te China): Dao produces one. One produces two. Two produces three. Three produces the ten thousand things. (In classical Chinese, the "ten thousand things" means "everything." Commentators have long disagreed over what the "one, two, and three" refers to, usually plugging in their favorite cosmological, cosmogonic, or metaphysical model.) Laozi further writes: Something amorphous & consummate existed before Heaven & Earth. Solitude! Vast! Standing alone, unaltering. Going everywhere, yet unthreatened. It can be considered the Mother of the World. I don't know its name, so I designate it "Dao." Compelled to consider it, name it "Great." (Dao is considered indistinct & undefinable.)
Buckland's Third Revolution poster column #5
Depending on the venue from which one's primary perspective is oriented (biology, astronomy, cosmology, mathematics, etc...), the above reference can be interpreted to coincide with subjectively embraced criteria for each of these (and other) interests. In other words, one can see basic criteria for different subjects in the quote.
 |
 |
Let us take a look at a preliminary mock-up of a timeline under construction, noting that in addition to the sparse examples, a larger effort will need to include additional timeline materials either integrated or overlayed, dealing with alternative pattern scenarios (numbers and otherwise), including references to extinction and re-evolution events such as those noted with oxygenation, meteorites/asteroids, ice/slush ball (glaciation/hydrothermal) ages, distance of moon, rotation of earth, movement and placement of earth in the larger galactic cyclicity, geo-magnetism etc..., in an effort to include as many variables as is needed for future reference that is readily available for consideration.
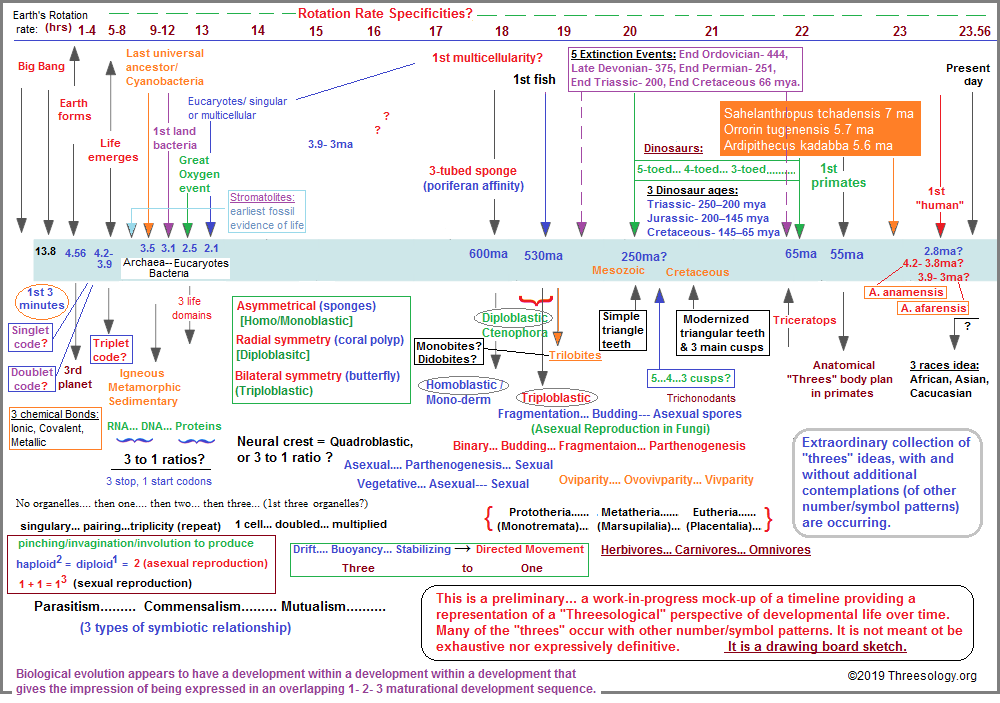
Some of the initial information was derived from: This Timeline Shows The Entire History of The Universe, And Where It's Headed. Other information was pieced together from this and that source by an effort of random internet/book browsing. You may want to argue about the events, the eras, and the rate of rotation, but the idea was to provide some semblance of factuality, even if the facts were derived from sources you might want to disparage as being questionable. Nonetheless, the information gives a generalized representation of the overall intent. If you disagree with the time intervals, that is your personal preference to do so. Likewise if you disagree with what may or may not have occurred in the sequence laid out. While such numbering interests will be important for a more comprehensive timeline construction, they are not particularly important for the present illustration meant as a generalization. And yes, I know a lot of things are left out. And yes I know other number and symbols variables can be... and should be included in a more comprehensive survey of developmental life and geology. And inasmuch as you might want to argue about finer details, again.... that is not the point of the presentation. More exacting details can be worked out. Lots of old, traditionalized and new information must be re-examined from a "Threesological" perspective. I intend to go through a lot of different kinds of information in and out of biology in the forthcoming pages.
The "Threesological" timeline profile describes "species" of cognitive thinking about biological development and associated events. Yes, it encompasses all the disciplines of thought as well as everyday considerations. One of the many ideas concerning biology is that called Punctuated Equilibrium proposed by Stephen J. Gould and Niles Eldredge. My point in bringing up this particular idea is prompted by an early morning walk with my brother Charlie accompanied by his dog Obie. We were walking past a high school baseball field when I noticed the words "Ball- Strike- out" on the scoreboard. The three-patterned reference on a baseball scoreboard recalled to mind the theory proposed by Gould and his interest in baseball. I mentioned the idea of punctuation to my brother just as my mind drifted onto a scene in which I could visualize Gould sitting musefully in the bleachers thinking about biology while immersed in the events of the game... many of which are long periods of lull that become "punctuated" by some event such as a strikeout, homerun, stolen base, etc. While he also spoke in terms of "walls" related to biological development... such as the Left, Center and Right field walls, he did not make the connection with the many threes which occur in Biology like those which occur in baseball.
For example, 3 strikes and your out. And let us mention the abbreviations of RBI (Runners batted in), GSH (Grand slam homer), and ERA (Earned run average). However, it would be remiss of me to fail to include non-three abbreviations which can be found here: Standard Baseball Stats. He also didn't identify (with biology) the presence of the 3-to-1 bases, in that the first three are enumerated (1st, 2nd, 3rd), while the so-called 4th base is routinely designated with a non-number reference called Home plate. If I had been there sitting beside him at the time (not that I actually watch baseball), I wonder if my "Threesological" timeline idea would have made any sense to him. One can only speculate. When I first heard about the "punctuated equilibrium" idea, it was obvious to me he was making a reference to experiences of baseball spectators. To myself I jokingly wondered what theory he might have come up with had he been the spectator of some other sport to use as a 'basis' (no pun intended) for creating a model of biological activity... Then again, perhaps human pastimes are symbolic (macro) representations of (micro) events because such patterns are embedded in our psyche in terms of the ability by which our brain makeup and activity can best describe such influences... as crude or refined as we might want to credit such an inference. However, the microscopic affecting the macroscopic and vice versa is a notion well-known by those who practice the "esoteric" arts such as astrology, tarot card reading, palmistry, weather forecasting, geology, medicine, philosophy, psychology, chemistry, butterfly effects, etc...
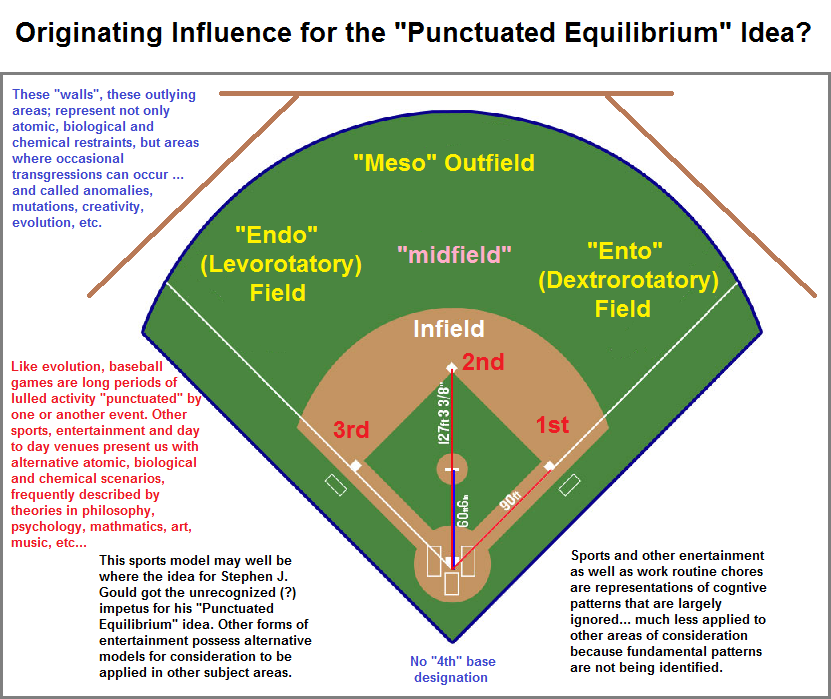
Yet, let me interject onto this 1st page of this series (though I have just begun to administer threes examples on the 15th page in this series), is the idea of making a comparison between biology and cycling, just as we might assume this is where Gould got his impetus for the notion of "Punctuated Equilibrium". A far better analogy between a sport and biology... at least in terms of applying more variables to the occasions under which biology can occur, is that of professional cycling. At this interjected writing, today is Sunday, the 8th of September at 10:19 AM. A younger brother (Charlie) and I were beginning to watch the tail end of the race in Spain called the Vuelta a España (Tour of Spain). As I had done on the aforementioned walk one morning concerning Gould and his interest in baseball, and after my brother said that watching cycling is watching baseball, I mentioned that cycling too could be used as a model for biology because of its "punctuated events". My brother made the comment (regarding cycling), that there were underlying tactics taking place that were not easily seen, which don't manifest themselves till later on. I then mused on the wide variety of terrains which cycling events may occur in, along with the occasional accidents, ongoing rivalries, and "extinctions" of some riders, not to mention those that obtain a "first place" position in which to gain notoriety by being given a jersey... a lineup presenting us with a 3 to 1 ratio:


Tour de France 2019
Since the triplet code of RNA and DNA, as well as the basic structures of proteins can be interpreted as 3-to-1 ratio structures, it is also fitting that I include the idea that instead of 3 Germ layers there are four, as counted by the authors of this article: Neural crest: The fourth germ layer by K. Shyamala, Sarita Yanduri, HC Girish, and Sanjay Murgod; as well as these alternative review sources:
- Chapter 1 - The Neural Crest, a Fourth Germ Layer of the Vertebrate Embryo: Significance in Chordate Evolution by Nicole M.Le Douarin and Elisabeth Dupin
- Neural crest: The fourth germ layer
- The neural crest and neural crest cells: discovery and significance for theories of embryonic organization by Brian K. Hall
- The neural crest as a fourth germ layer and vertebrates as quadroblastic not triploblastic by Brian K. Hall
Is the neural crest to be viewed as a fourth germ layer or as a branched relative of the mesoderm (which came third in its evolutionary role)? Here is a reference to a specificity of the Neural crest in the Zebra fish and associated comments:
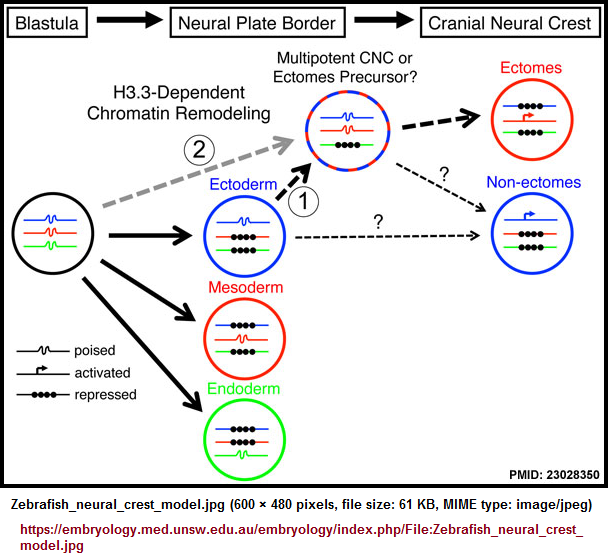 |
At the early embryonic blastula stage, cells have a broad potential with cis-regulatory elements for developmental genes existing in a "poised" chromatin state. After gastrulation occurs to form the three major germ layers (ectoderm, mesoderm, and endoderm), genes associated with a particular germ layer are activated or maintained in a poised state, whereas genes for other layers are strongly repressed at the chromatin level. The cranial neural crest (CNC) is unusual in that it is derived from ectoderm yet can give rise to mesoderm-like derivatives such as skeleton. H3.3-dependent histone replacement could thus be required to remodel the enhancers of mesodermal genes needed for ectomesenchymal fates, with the distinctive role of H3.3 in CNC correlating with the need to depress mesodermal enhancers that have been previously silenced in the ectoderm germ layer. Alternatively H3.3 incorporation could act to maintain mesoderm-like potential in the CNC ectoderm from an earlier time in development. It also remains unresolved the extent to which ectomesenchyme derivatives (e.g. head skeleton) and non-ectomesenchyme derivatives (e.g. pigment, glia, and neurons) derive from a common multi-potent precursor. Hence, the cranial pigment and ectomesenchyme defects of h3f3adb1092 mutants could arise from altered histone replacement in a common multi-potent precursor, or alternatively from independent defects in different subsets of heterogeneous CNC with more limited potential. |
Unless we want to assume that our many observations of singularity, diplicity (biplicity), triplicity, quadriplicity, etc... are little more than arbitrary assignments (including the very many instances where such patterns are taking place in a step-wise fashion), then there must be a reason(s) for such— and this reason may be strictly or at least partially due to environmental processes which represent constraints... otherwise we would have more pattern models than we do. If it is environmental, and we note that the environment changes and biology adapts to such changes, then predictability about changes may well lead us to predict forthcoming biological directions of change. Such a process of cataloguing enumeration will enable us to add mathematical models which will assist in the development of a theoretical discipline of biology. An excellently elaborated discussion of this is provided below:
Wenying Shou, Carl T. Bergstrom, Arup K. Chakraborty, Frances K. Skinner Editorial Jul 14, 2015
Theoretical ideas have a rich history in many areas of biology, and new theories and mathematical models have much to offer in the future. Main textWhen scientists want to explain some aspect of nature, they tend to make observations of the natural world or collect experimental data, and then extract regularities or patterns from these observations and data, possibly using some form of statistical analysis. Characterizing these regularities or patterns can help scientists to generate new hypotheses, but statistical correlations on their own do not constitute understanding. Rather, it is when a mechanistic explanation of the regularities or patterns is developed from underlying principles, while relying on as few assumptions as possible, that a theory is born. A scientific theory thus provides a unifying framework that can explain a large class of empirical data. A scientific theory is also capable of making predictions that can be tested experimentally. Moreover, a theory can be refined in the light of new experimental data, and then be used to make new predictions, which can also be tested: over time this cycle of prediction, testing and refinement should result in a more robust and quantitative theory. Thus, the union of empirical and quantitative theoretical work should be a hallmark of any scientific discipline.
Theory has long been celebrated in the physical sciences, but the situation is very different in the life sciences. As Conrad Hal Waddington wrote in 1968, in the preface of Towards a Theoretical Biology: ‘Theoretical Physics is a well-recognized discipline, and there are Departments and Professorships devoted to the subject in many Universities. In strong contrast to this situation, Theoretical Biology can hardly be said to exist as yet as an academic discipline. There is even little agreement as to what topics it should deal with or in what manner it should proceed’. Yet theory plays a paramount role in biology. The best known example of a theory in biology is, of course, the theory of evolution by natural selection. Charles Darwin may have been a globe-trotting hands-on naturalist and geologist, but his outstanding contribution to science was theoretical. Drawing on fieldwork, fossil records and the breeding records of domestic animals and plants, he observed that variations readily arose and that much of this variability was heritable. After reading Malthus' essay on the repercussions of an exponential growth in population, Darwin reasoned that a struggle for existence must have selected for the variants that were most adapted to their local environment. As different populations adapted to different environments, he argued that these variations accumulated over time, eventually forming diverse species. Despite the success of his theory, Darwin never formalized it in mathematical terms. Rather, he wrote: ‘I have deeply regretted that I did not proceed far enough at least to understand something of the great leading principles of mathematics; for men thus endowed seem to have an extra sense’ (May, 2004). Although a theory does not have to be formulated as a mathematical model to be useful, the development of such a model is a hallmark of a maturing theory. The role of theory and mathematical models in the life sciences is the focus of this editorial. By the end of the 1960s, when Waddington was bemoaning the lowly status of theoretical biology, the field had in fact witnessed major breakthroughs. Early population geneticists such as Pearson, Fisher, Wright and Haldane had developed the formulation that Darwin was unable to construct, providing a mathematical foundation for the theory of evolution by natural selection. In the process, they also generated a number of major advances in statistics. The modern evolutionary synthesis had reconciled the gradualist Darwinian view of natural selection with a Mendelian understanding of genetics, unifying observations from naturalists, experimental geneticists and paleontologists. A crucial contribution from theory came in 1943 when Luria and Delbrück used mathematical reasoning and experiments to conclude that mutations arose in the absence of selection, rather than in response to selection. And in 1953 the structure of DNA was determined with the help of a theoretical physicist and the building of physical models (which were the forerunners of today's computer simulations). Elsewhere, the simple and elegant Lotka–Volterra models of competition and prey-predation had jump-started theoretical ecology, Kermack–McKendrick theory had laid a foundation for mathematical epidemiology, and Burnet had developed the clonal selection theory that lies at the heart of our understanding of the adaptive immune system. In neuroscience it is difficult to overstate the importance of the Hodgkin–Huxley model of action potentials or Rall's use of cable theory to provide a framework for understanding the complex, dendritic structures of neurons. During the past half-century, theory has continued to advance in diverse areas of biology. Within evolution and ecology, for example, evolutionary game theory provided a framework for thinking about the evolution of strategic behavior, while kin selection and multi-level selection theory helped to explain cooperation and altruism. Life history theory offered a systematic way to think about the evolution of senescence, developmental plasticity and reproductive schedules, among other things, while optimal foraging theory introduced economic reasoning into the study of animal foraging. Other examples include kinetic proofreading in biochemistry, the Hopfield model of neural networks, and the use of bifurcation theory and phase-plane analyses in neuroscience. Increased computational power has also allowed biologists to study the structure and function of proteins, and to simulate complex biological processes such as morphogenesis, chemotaxis, the cell division cycle, metabolism and, in some cases, the workings of the entire cell. And over the past decade new experimental tools and techniques have generated such a staggering amount of data that we are, in the words of Sydney Brenner, ‘thirsting for some theoretical framework with which to understand it’ (Brenner, 2012). This is true in genetics and genomics, immunology, microbiology, neuroscience and many other areas. New theoretical and computational models are therefore needed to make sense of this abundance of data. Yet, despite this rich history, the divide between theoretical and empirical biologists seems to persist, even in areas with a long history of both types of work, such as ecology and evolutionary biology (Haller, 2014). One reason for this is that the complexity of real biological systems often requires relatively sophisticated mathematics, which means that many theoretical papers do not resonate with empirical biologists. This complexity has many sources: the number of interacting parts in even the simplest living cell presents a formidable challenge for a theoretical biologist, as does the heterogeneity that is intrinsic to biological systems. Moreover, interactions among these parts can span a large range of time scales (from picoseconds for electron transfer in photo-chemical reactions, to billions of years for evolution) and length scales (from molecules to cells, from organisms to ecosystems). As a result, theoretical biologists often need to make a trade-off between abstraction and realism (or between the qualitative and the quantitative) when building mathematical models. The appropriate level of abstraction will depend on the question of interest. For example, simplifying assumptions can be made to develop a highly abstract model that reveals general features shared by many systems and thus improves our understanding of some aspect of biology. However, such a model is unlikely to produce quantitative predictions for any particular system. On the other hand, a highly detailed model that contains many equations and parameters is unlikely to improve intuitive understanding of a system or process. However, if the various parameters in the model can be measured to a credible level, then these models should be able to make quantitative predictions about a given system or process. Part of the challenge in model building is to choose the right level of abstraction despite the complexity of biological processes. In other words, we need to work out what aspects of this biological complexity we can ignore and still gain critical insights about a biological phenomenon. So how can we increase interactions and collaborations between theoretical biologists and empirical biologists for the benefit of the discipline as a whole? First, universities and institutions should ensure that biology students are taught more about theoretical and mathematical techniques, including ideas from physics that have already been successfully applied to biological questions (such as statistical mechanics and nonlinear dynamics). Laboratory work could also be extended to include exercises that involve computer simulations. These changes would help biologists to better communicate with theorists and, more importantly, to incorporate quantitative thinking into their own work. There are signs that this is starting to happen: the sixth edition of Molecular Biology of the Cell, for example, includes examples where ordinary differential equations are used to model gene regulation and to explain switch-like and oscillatory dynamics. It would be good to see more mathematics in biology textbooks. Second, theoretical biologists could do more to increase the chances that their papers will resonate with empirical biologists. The primary audience for some theory papers will be other theorists, and like all papers aimed at a specialist readership, these papers will be a challenging read for non-specialists. However, the potential impact of most theoretical papers—especially modeling papers—could be increased by following a few simple guidelines. The first thing to do is to clearly state the goal of the modeling: is the aim to organize data emerging from high-throughput experiments, to test a particular hypothesis, to uncover the basic mechanisms driving some phenomenon, to evaluate the feasibility of an intuitive argument, to make specific predictions, or something else? How does the model or theory relate to and differ from previous models, and what are its advantages and disadvantages? What assumptions have been made, and what are the justifications for these? How were the parameters in the model chosen? Mathematical papers can be made more accessible by giving step-by-step derivations for equations, and intuitive explanations for how these equations reflect the biological process under investigation, even if this involves covering material that may already be familiar to other theoretical biologists. Schematic diagrams can also help. Finally, it is important to relate the conclusions back to biology. This includes clearly stating which conclusions are not surprising (in the sense that they are straightforward derivatives of the empirical results used to constrain a model), which insights are novel, and which predictions are worthy of empirical tests. Theoretical biologists can also benefit from wet lab experience to help them appreciate what doing an experiment involves. Third, empirical biologists could make their work more accessible and valuable to theorists. For example, all the relevant datasets should be included in papers. Moreover, where possible, time-course data should be collected, rather than just ‘end-point’ data, as this will allow dynamical processes to be studied. And when the experimental measurements in a paper differ from previous measurements in a significant way, it would help theorists (and others) to build on the work if the authors discussed possible reasons for these differences. Taken together the recommendations outlined above should lead to improved collaboration between theoretical and empirical biologists. ELife welcomes theoretical and modeling papers in all areas of biology, especially papers that report new biological insights, make substantial predictions that can be tested, or help to resolve contradictory empirical findings. Papers that report new theories or algorithms that have the potential to solve important biological problems are also welcome. Papers can also be as long (or as short) as necessary. Across the life sciences we aim to publish papers that are insightful and change the way that other researchers think about their subject (Malhotra and Marder, 2015). Theory and modeling are no exception. |
Simply put, we need ideas which think outside the conventional boxes of modeling that biologists have gotten themselves entangled with that are creating a fossilized species of biology. A "Threesological" approach is an attempt to dig them out of the rut and provide a framework for an adventurous spurt of growth and further speciation into uncharted territories...because there is far too much territorialism that has taken place.
In viewing what may loosely be called a "Threesological imperative" since we can recognize a recurrence of such a pattern in many subject areas, the usage of a proposed timeline of threes events is a classification system which can assist in the identification and distribution of other patterns... many of which are already acknowledged and are set out on their own respective timeline representations. However, instead of referencing the presence of one or another number patterns over time and across subject genres, words and other labeling methods are utilized... perhaps to conceal what might otherwise be viewed as an exercise in some numerological scheme of differentiation. The usage of a timeline for registering the occurrence and absence of "threes" as well as other number (and non-number used) patterns can help to facilitate identification of similarities not now being considered as a dimension of occurrence with biology and non-biological events. If there is a recurring 1-2-3 developmental sequence, the word "developmental" must be defined beyond the present scope of typical biological definitions. If we say that the 1-2-3 sequencing is simply a matter of "normal" aggregation like the process of life over time, then why has the aggregation stopped, and why does the small number sequences repeat... such as why isn't the triplet code of DNA and RNA evolving towards more aggregations to reveal a quadruple, quintuplet, etc... coding system? What is sustaining the repetition and what created this pattern in the first place?
With respect to the development of a timeline, one must decide if they will use a Horizontal (left to right/ right to left) approach, a Vertical (Hierarchical... top to bottom/ bottom to top) approach, or a Diagonal (left top/bottom to right bottom/top) approach. Then again, two or all of them might well be applied in some instances. There are of course other models such as a tree or branching system, but for the purposes of a simplified form, a left to right horizontal frame works. From this point I want to include the origin of the Universe up to the development of humans, but do not want to include much in the way of everyday human expressions that do not expressly deal with biological development... even though pre-biological examples can be given which lead up to the development of life such as in the case of chemical compounds. Whereas all the examples to be given actually are human-spun ideas, they are ideas related to attempts at being objective about biological development. This includes noting that life as we know it has occurred on the 3rd planet from a source of solar energy. So let us begin with a preliminary illustration:
To think that nature does not use numbers or other patterns in its own way (since, realistically, it is humans which create the labels for patterns and the orientations thereof), is actually quite silly to think that nature defers to the organizational methods of the human brain and not the other way around. This is but another example of the old ego-centricity denoted by the ideas of the Sun revolving around the Earth and Kingdoms being drawn on a map in a centralized position as an expressed feeling that the world revolves around a particular kingdom. The timeline will help to establish a means to measure variances of occurrence, whereby an acknowledgement of limitations will be noted so that the reasons for such can be understood. Indeed, it should be understood that a "Threesological" approach may or may not be the development of a new science, whereas it may come to either consume or be consumed by an already existing science (all sciences, religions, governments, businesses, etc... are predatory). You may or may not like it... but it is here... call it a weed, a flower or something non-biologically framed... it nonetheless has arisen.
Origination date: Tuesday, June 25, 2019... 4:41 AM
Initial Posting: Sunday, September 8th, 2019... 11:17 AM
Updated Posting: Tuesday, January 17th, 2023... 11:38 AM
Herb O. Buckland
herbobuckland@hotmail.com