Threesology Research Journal

Threesology Research Journal: Dualities and Simplistics in Mathematics Dualities and Simplistics in Mathematics
page 3

Visitors as of 2/27/2021

What I am trying to accomplish is to show that not only is there an over-riding reliance of patterns-of-two in mathematics, but provide examples of patterns-of-three as a contrast. If you are not firmly conscious of how frequent patterns-of-three crop up in different subjects in different guises, the presence of patterns-of-two may not likewise be firmly acknowledge and represent a primivity of conceptualization as does the over-riding reliance of "twos" in economics which brings humanity recurring problems. This statement needs to be restated on each of the dualities pages because they do not explicitly focus on patterns-of-two alone.

Let us look at some more specific examples of dichotomization in Mathematics, and add alternative ideas involving patterns-of-three as a type of contrast.

Rational/Irrational numbers
Integer/Opposite, as in opposite number... the word "Outeger" has not yet been devised, nor a corresponding "Midteger", equivalent to the ideas of In, Out, Middle
Fractions/Whole Numbers
Greater than or equal to (⋝)/ Less than or equal to (⋜)
Greater than (>)/ Less than (<)
Very much greater than (⋙)/ Very much less than (⋘)
Plus - Minus (±)/ Minus - Plus (∓)
2- 3 -4 triple ensemble: square root, cube root, fourth root... (by including the nth root[radical], we have a 3 to 1 ratio)
per-million (ppm), per-billion (ppb), per-trillion (ppt) Math Symbols List
Much less then (≪)/ Much greater than (≫)
Synthetic (2)/ Analytic (1 and 1...)
Summation (∑) / Double Summation (∑∑)... no triple summation
lower / first quartile (Q₁); median / second quartile (Q₂); upper / third quartile (Q₃)
Therefore (∴)/ Because / since (∵)
one dot, multiply and decimal separator (⋅), two dots, ratio (∶) and division, three dots, therefore/ because (∴/ ∵), four dots, proportion (∷). There are no five, six, etc., dot configurations.
A priori (prior to)/ A posteri (afterwards)
Irrationality of the square root of 2 (√²)
Increment (++)/ Decrement (--)
∈ (element of)/ ∉ (not an element of)
start an equation/ finish an equation... (or get hung up somewhere in between)
≤ (less than or equal to)/ ≥ (greater than or equal to)
⊂ (subset of)/ ⊄ (not a subset of)
The opposite of finding the square root of a number is squaring the number. Squaring a number means multiplying the figure by itself. For example, the square root of four is two, and two squared is four. Squaring is the same as raising a number to the power of two. ( What Is the Opposite of a Square Root?)
∝ (proportional to)/ inverse proportionality
super-script/sub-script
Real numbers/Imaginary numbers
There is no math symbol representing infinitesimal, but there is for infinity: ∞
In his book Analysis Vol. 1, author Terence Tao argues that while each natural number is finite, the set of natural numbers is infinite (though has not defined what infinite means yet). Using Peano Axiom, if a property holds for P(0) and whenever P(n) is true, P(n+1) is also true, then it is true for all natural numbers. ( Why set of natural numbers is infinite, while each natural number is finite?)
true/false
valid equation/false equation
Responsive/ Unresponsive yo-yos (I include this dichotomy for fun)
↑ (up arrow)/↓ (down arrow)
→ (right facing arrow)/ ← (left facing arrow)
greater than/less than... equal to
superior/inferior equations
arithmetic... algebra... geometry... calculus
numbers... letters... lines... symbols
in-tegers, but no ou-tegers (nor mid-tegers)
signs and symbols as scratch marks
"PEMDAS" - Please Excuse My Dear Aunt Sally. / "GEMDAS" - Give Everyone More Delicious AppleSauce. Exponents and the Order of operations

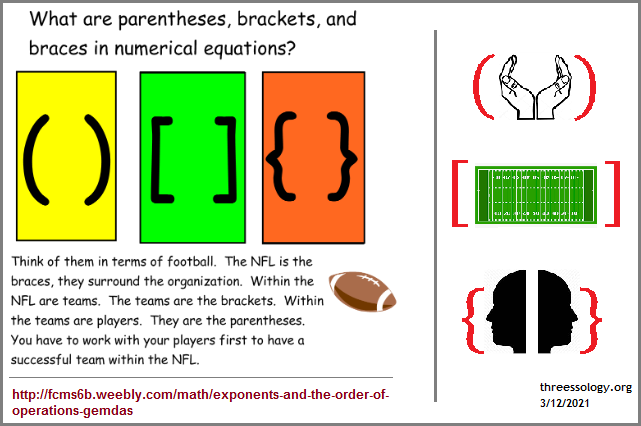
Parenthesis, Brackets, and Braces analogy

The order of operations, which is used throughout mathematics, science, technology and many computer programming languages, is expressed here:

exponentiation and root extraction
one horizontal line, minus... (−), two horizontal lines, equal... (=), three horizontal lines, identity sign: specialized equality... (≡), 4 horizontal lines, strictly equivalent to... (≣)HTML symbols
Single integral (∫), Double integral (∬), Triple integral (∭) (no quadruple, etc., integral)
multiplication and division
addition and subtraction

This means that if, in a mathematical expression, a sub-expression appears between two operators, the operator that is higher in the above list should be applied first. The commutative and associative laws of addition and multiplication allow adding terms in any order, and multiplying factors in any order—but mixed operations must obey the standard order of operations. Order of operations

Equations which (symbolically) reference the three sentence ending marks: period. question mark? exclamation point!
Pure mathematics dealing with nouns: person- place- thing; or the pre- present- post variations
We have the single indent: (small p- prime) ′, and double indent (large P- prime) ″, but no triple indent symbol
Exact/proportional... approximation
additive/additive inverse (add/subtract)
± (plus and minus sign)/ ∓ (minus and plus sign) (yet no multiply an divide or divide and multiply sign?)
An irrational number is a number that cannot be expressed as a fraction p/q for any integers p and q. Irrational numbers have decimal expansions that neither terminate nor become periodic. Every transcendental number is irrational. Wolfram Math World: Irrational number
Integer: is a whole number (not a fractional number) that can be positive, negative, or zero.
probability/improbability
possibility/impossibility

Word substitutions:

product by multiplication
sum by addition
difference by subtraction
quotient by division (quotient means "how many times"... it is a three-patterned expression) [let us include the word "factor" related to division]

Associative, Commutative, Distributive, Identity (Properties of addition)... as a counting sequence:
1. (0) Identity Property: The sum of any number and zero is the original number. For example 5 + 0 = 5.
2. (1) commutative property: when two numbers are added, the sum is the same regardless of the order of the addends. for example 4 + 2 ="2" + 4
3. (2) Distributive Property: The sum of two numbers times a third number is equal to the sum of each addend times the third number. For example 4 * (6 + 3) = 4*6 + 4*3
4. (3) Associative Property: When three or more numbers are added, the sum is the same regardless of the grouping of the addends. For example (2 + 3) + 4 = 2 + (3 + 4).

List of constants: list of physical constants

Some "three" approximations references from different orientations (

Constants hovering around the "3" area.)

Three types of Percent Problems:

Find the unknown amount in a percent problem
Find the unknown rate in a percent problem
Find the unknown base in a percent problem

π (pi) = 3.14
Wien entropy displacement law constant: 3.002916077
parsec = 3.26 light years
3 billion base pairs: figure typically given for the human genome
...about 3% of the complete genomes between humans and chimpanzees differ by deletions, insertions and duplications. Human evolutionary genetics
human adult brain: approx. 3 lbs
Average walking speed: roughly 3 miles per hour (some say 3 to 4, making allowances for age, height, etc...)
Cosmic background radiation = 3k (other sources say 2.7)
Interrogation/Witness questioning reference: 3rd degree
3rd eye: The third eye refers to the gate that leads to the inner realms and spaces of higher consciousness. In spirituality, the third eye often symbolizes a state of enlightenment or the evocation of mental images having deeply personal spiritual or psychological significance. Third Eye
3rd Ear: The "third ear," a concept introduced by psychoanalyst Theodor Reik, refers to the practice of listening for the deeper layers of meaning in order to glean what has not been said outright. It means perceiving the emotional underpinnings conveyed when someone is speaking to you. The Third Ear
First hand eyewitness account; Second hand: previously used, not new; Third hand (Typically defined in different ways as being twice removed from an original. I did not find an account which references the mouth being used as a third hand, or the usage of other items used in the manner of an additional hand for support.)
3rd leg: penis and walking stick or cane
nose "3rds": The length of the nose can be divided into thirds. The upper third is composed of the nasal bones. The middle third is composed of the upper lateral cartilages; and the lower third is the tip, which is composed of the alar cartilages. Nose Surgery; Rhinoplasty Anatomy
Emoticon ":3" (representing a cat or cute/coy face)
3 fish mouths: Most fish mouths fall into one of three general types: Superior, or sometimes called supra-terminal, mouths are upturned. Terminal mouths point straight forward and are the most common mouth type. Inferior, or sub-terminal, mouths are turned downward. Fish Mouth Types and Their Uses
3 brain divisions: The brain can be divided into three basic units: the forebrain, the midbrain, and the hindbrain. The hindbrain includes the upper part of the spinal cord, the brain stem, and a wrinkled ball of tissue called the cerebellum (1). The hindbrain controls the body's vital functions such as respiration and heart rate. Brain Basics: Know your brain.
Length of a meter using the speed light: So in 1983 it was decided to define the meter from the speed of light. This made the speed of light (in a vacuum) 299,792,458 m/s by definition. As a result, if you try to measure the speed of light, you are actually measuring the length of a meter. Light Meter by Brian Koberlein, 16 Dec. 2012
The enhanced (Tornado Measurement) F Scale (EF Scale) was implemented in the United States on February 1, 2007. The EF scale uses three-second wind gust estimates based on a more detailed system for assessing damage, taking into account different building materials. Measuring Tornadoes: The EF scale
3 types of mathematics: Modern mathematics can be divided into three main branches: continuous mathematics, algebra, and discrete mathematics. The division is not exhaustive. It is difficult to exactly fit some fields, such as geometry or mathematical logic, into any of these categories. Three Types of Mathematics.
3 elements of Combinatorics: "greatest", "smallest", "optimal". BYJU's Combinatorics
3 types of Geometries: In two dimensions there are 3 geometries: Euclidean, spherical, and hyperbolic. The Three Geometries

Combinatorics is a branch of mathematics which is about counting – and we will discover many exciting examples of "things" you can count. First combinatorial problems have been studied by ancient Indian, Arabian and Greek mathematicians. Interest in the subject increased during the 19th and 20th century, together with the development of graph theory and problems like the four colour theorem. Some of the leading mathematicians include Blaise Pascal (1623 – 1662), Jacob Bernoulli (1654 – 1705) and Leonhard Euler (1707 – 1783). Combinatorics. Consider the 3 Combinatorics categories:

Factorials: Combinatorics can help us count the number of orders in which something can happen.
Permutations: Refers to possibilities or alternatives in a specific order.
Combinations: Refers to probabilities of the possibilities without respect to a specific order.

When the order doesn't matter, it is a Combination./ When the order does matter it is a Permutation. Combinations and Permutations
Samples with replacement versus samples without replacement: Combinatorial Probabilities
Differential calculus (cuts up pieces)/ Integral calculus (puts the pieces together); limits- derivatives- integration/integrals
Mononomial equations/ Polynomial equations
Sequence (parts)/ Series (whole): A sequence is a set of numbers which are written in some particular order. A series s is something we obtain from a sequence by adding all the terms together. Arithmetic and geometric progressions.

In mathematics there are three different types of progressions: Arithmetic Progression

Arithmetic Progression (AP)
Geometric Progression (GP)
Harmonic Progression (HP)

Three major forms of linear equations: point-slope form, standard form, and slope-intercept form. Forms of linear equations review

There are three possible outcomes for a system of linear equations: one unique solution, infinitely many solutions, and no solution.

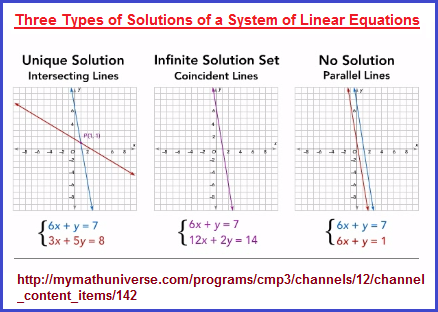
Three Types of Solutions of a System of Linear Equations

Degree of a Polynomial Names of polynomials by degree:

Special case – zero (The degree of the zero polynomial is either left undefined, or is defined to be negative (usually -1 or -∞).)
Degree 0 – non-zero constant]
Degree 1 – linear
Degree 2 – quadratic
Degree 3 – cubic
Degree 4 – quartic (or, if all terms have even degree, biquadratic)
Degree 5 – quintic
Degree 6 – sextic (or, less commonly, hexic)
Degree 7 – septic (or, less commonly, heptic)

For higher degrees, names have sometimes been proposed, but they are rarely used:

Degree 8 – octic
Degree 9 – nonic
Degree 10 – decic

Names for degree above three are based on Latin ordinal numbers, and end in -ic. This should be distinguished from the names used for the number of variables, the arity, which are based on Latin distributive numbers, and end in -ary. For example, a degree two polynomial in two variables, such as x²+xy+y², is called a "binary quadratic": binary due to two variables, quadratic due to degree two. There are also names for the number of terms, which are also based on Latin distributive numbers, ending in -nomial; the common ones are monomial, binomial, and (less commonly) trinomial; thus x²+y²x²+y² is a "binary quadratic binomial".

HoB Note: This list speaks of the aforementioned "conservation" effect taking place with human cognition due to what is thought to be the influence of an incremental deterioration of environmental events creating conditions whereby life forms must adopt conservative methods for survival.

Subset (⊂)/ Not a Subset (⊄)
Superset (⊃)/ Not a Superset (⊅)
Percent (%), Per mille (), Per Ten thousand (‱)
Numerator (above the line)/Denominator (below the line); (A vertical slanted line may mean ratio or divided by, but there is no similar usage as that seen when a horizontal line is used.)
One vertical line may mean divided by. Two vertical lines may mean parallel to. There appears to be no symbol expressing three vertical lines.

Neither has mathematics advanced far enough for mathematicians to compute equations using multiple marks such as displayed by the I-Ching where multiple (2-line combinations of three lines) are called Trigrams, but are actually Bi-grams because there is no 3-part segmented line being used in any of the I-Ching configurations. Such configurations have been aligned with amino acids, but not with mathematics since mathematicians do not have such a formula being considered as a standard way of thinking. However, here is one very simple attempt to proceed along the application of mathematics to the I Ching: Combinatorics of the I Ching by Brian S. Kimerer

Kimerers usage of Bigrams in his Combinatorics example does not look past the fact that the presence of two-line combinations (single and double lines) actually references a Bigram and is in reality masquerading as a Trigram by using combinations of three 2-line illustrations. Like an ancient primitive whose largest counting number was actually "2" but referenced the idea of larger numbers with the word "Trigram".

Trigrams or Bigrams?Bigrams impersonating Trigrams

Exponent, but no Inponent or Mid/Mesoponent
equal/ not equal
Prime/ anti-Prime (Highly composite number): 5040 and other Anti-Prime Numbers - Numberphile
ordered/ unordered
Matter/anit-matter
Gravity/ anit-gravity (Dark energy)?
Positive energy/ negative energy (casamere effect)?
positive mass/ negative mass?
qualitative/quantitative
less than/ more than (strict inequality)
exclusion/inclusion inclusion–exclusion principle (Include 1, exclude 2, include 3, exclude 4, include 5, ...include/exclude to ∞)... to find the cardinality of the union of n sets:
1. Include the cardinalities of the sets. (1)
2. Exclude the cardinalities of the pair-wise intersections. (2)
3. Include the cardinalities of the triple-wise intersections. (3)
4. Exclude the cardinalities of the quadruple-wise intersections. (4)
5. Include the cardinalities of the quintuple-wise intersections. (5)
6. Continue, until the cardinality of the n-tuple-wise intersection is included (if n is odd) or excluded (n even).
Prime numbers but no primordial or post-mordial numbers
always equal/sometimes equal
identity (confirmed)/ identity (enigma or mystery)
symmetrical (balanced)/unsymmetrical (unbalanced)
Three types of symmetry : reflection (bilateral), rotational (radial), and translational symmetry. (Equations can be viewed as "life forms" exhibiting one, another, or all three forms of symmetry)
Substitution ciphers: one letter of the alphabet represented another letter (duality)

The "life forms" of equations can be viewed as body plans, or schematics, or scaffolding, or architecture, or line drawing, or musical score, etc... Thus, with respect to body plans, equations can represent bilateral, radial and/or spherical.

Body plans can be seen as monoploblastic (let us say as sponges... though there is controversy over this), bi- or di-ploblastic, and triploblastic, related to the quantity of Germ layers. As such, present mathematics equations are on a very primitive level of development. There is greater complexity yet to evolve... but present institutions of mathematics are actively suppressing the development of mathematics like the antiquated ideas imposed on ancient peoples of the past. Present day mathematicians are much like the priests of old who wield a very strict hold on ideas breeching their control or ability to visualize.

The 1- 2- 3 developmental sequence can already be seen as expressions in mathematics, yet in primitive models of representation, like the ooey-gooey osse of presumed past developmental sequences having occurred in the primordial soup/broth.

In some instances, there are multiple expressions regarding references to both "two-patterned" and three-patterned ideas that a complete reference of them in context needs to be reviewed. However, the problem with doing so is that if a person reading it is not familiar with identifying such patterns, they can easily overlook them. Yet, in making a reference to the existence of such and placing them into a context such as the present one, may well be enough of a directional beacon to bring them to light and thus organized as examples of the overall point I am trying to make about not only the primivity of mathematics, but the need to follow up in designing a new type.

The following falls on heels of the Theory of Equations:

In mathematics, Galois theory, originally introduced by Évariste Galois, provides a connection between field theory and group theory. This connection, the fundamental theorem of Galois theory, allows reducing to group theory certain problems in field theory; this makes them simpler in some sense, and allows a better understanding.

Galois introduced the subject for studying roots of polynomials. This allowed him to characterize the polynomial equations that are solvable by radicals in terms of properties of the permutation group of their roots—an equation is solvable by radicals if its roots may be expressed by a formula involving only:

Integers (Whole numbers and Negative numbers, but no fractions.)

nth roots An nth root of a number x is a number r which, when raised to the power n, yields x: rⁿ = x... or, for example: 3 is a square root of 9, since 3² = 9, and -3 is also a square root of 9 since (-3)² = 9.

Four basic arithmetic operations (Addition, subtraction, multiplication, and divisions.

This widely generalizes the Abel-Ruffini theorem, which asserts that a general polynomial of degree at least five cannot be solved by radicals (Square root, cube root, etc...

Galois theory has been used to solve classic problems including showing that two problems of antiquity cannot be solved as they were stated (doubling the cube and trisecting the angle), and characterizing the regular polygons that are constructible (this characterization was previously given by Gauss, but all known proofs that this characterization is complete require Galois theory).

Note: in the foregoing it is stated "two problems of antiquity", yet this article states there are Three classical construction problems of antiquity:

Squaring the Circle. Given a circle, construct a square that has exactly the same area as the circle.
Trisecting an Angle. Given an angle, construct an angle whose measure is exactly 1/3 the measure of the original angle.
Doubling a Cube. Given the length of the side of a (three-dimensional) cube, construct a length so that a cube with an edge of this length will have exactly double the area of the original cube.

Page initially created: Wednesday, March 3rd, 2021... 1:19:25 PM
Page initially posted: Saturday, May 22nd, 2021... 7:16 AM
Updated page: Monday, December 6th, 2021... 6:25 AM

Your Questions, Comments or Additional Information are welcomed:
Herb O. Buckland
herbobuckland@hotmail.com