
Page 11
http://threesology.org
Note: the contents of this page as well as those which precede and follow, must be read as a continuation and/or overlap in order that the continuity about a relationship to/with the typical dichotomous assignment of Artificial Intelligence (such as the usage of zeros and ones used in computer programming) as well as the dichotomous arrangement of the idea that one could possibly talk seriously about peace from a different perspective... will not be lost (such as war being frequently used to describe an absence of peace and vice-versa). However, if your mind is prone to being distracted by timed or untimed commercialization (such as that seen in various types of American-based television, radio, news media and magazine publishing... not to mention the average classroom which carries over into the everyday workplace), you may be unable to sustain prolonged exposures to divergent ideas about a singular topic without becoming confused, unless the information is provided in a very simplistic manner.
Another example of binary imaging is in the event of double refraction:
Also called birefringence, (double refraction is) an optical property in which a single ray of unpolarized light entering an anisotropic medium is split into two rays, each traveling in a different direction. One ray (called the extraordinary ray) is bent, or refracted, at an angle as it travels through the medium; the other ray (called the ordinary ray) passes through the medium unchanged. Double refraction can be observed by comparing two materials, glass and calcite. If a pencil mark is drawn upon a sheet of paper and then covered with a piece of glass, only one image will be seen; but if the same paper is covered with a piece of calcite, and the crystal is oriented in a specific direction, then two marks will become visible. 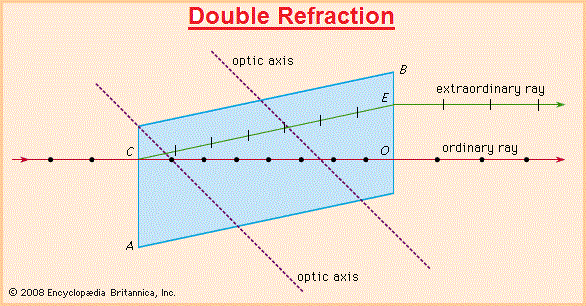 The (above) Figure shows the phenomenon of double refraction through a calcite crystal. An incident ray is seen to split into the ordinary ray CO and the extraordinary ray CE upon entering the crystal face at C. If the incident ray enters the crystal along the direction of its optic axis, however, the light ray will not become divided. In double refraction, the ordinary ray and the extraordinary ray are polarized in planes vibrating at right angles to each other. Furthermore, the refractive index (a number that determines the angle of bending specific for each medium) of the ordinary ray is observed to be constant in all directions; the refractive index of the extraordinary ray varies according to the direction taken because it has components that are both parallel and perpendicular to the crystal's optic axis. Because the speed of light waves in a medium is equal to their speed in a vacuum divided by the index of refraction for that wavelength, an extraordinary ray can move either faster or slower than an ordinary ray. All transparent crystals except those of the cubic system, which are normally optically isotropic, exhibit the phenomenon of double refraction: in addition to calcite, some well-known examples are ice, mica, quartz, sugar, and tourmaline. Other materials may become birefringent under special circumstances. For example, solutions containing long-chain molecules exhibit double refraction when they flow; this phenomenon is called streaming birefringence. Plastic materials built up from long-chain polymer molecules may also become doubly refractive when compressed or stretched; this process is known as photoelasticity. Some isotropic materials (e.g., glass) may even exhibit birefringence when placed in a magnetic or electric field or when subjected to external stress. Source: "Double refraction." Encyclopædia Britannica Ultimate Reference Suite, 2013. |

We might want to consider that the idea of double refraction mutated into an applied triple refraction ideology will have a significant application in space flight in a ship or by way of teleportation. The double refraction phenomena is an example of a switch. When I look at the image of a color spectrum, I see the activation of different switches. In other words, the observed differences in color are different switches. Likewise for molecular handedness and the existence of all atomic particles. Likewise for the appearance of one or another gender being born. The different human races, different religions, etc., etc., are expressions of different switches. However, with respect to handedness, most people may not include the notion of ambidexterity as a third option because they are inclined to observe and interpret the world in a binary (dual) fashion, and may even become angry when you point out a third consideration that they may come to be belligerently dismissive about.
On and off, input and output, etc., are different labels describing a "two" reference for which actions and action potentials may not be described with a distinct binary reference... and only provide a single idea such as impulse, reflex, instinct, motivation, reaction, dynamic, etc... Although we may be able to distinguish a polar opposite to any singular description, it is not necessarily named. We are aware of "verbs" (action, occurrence, state of being) and "adverbs" (verb modifiers), as well as other parts of sentence structure such as nouns (persons- places- things), pronouns, adjectives, etc... With respect to verbs and the three tenses (past [rung]- present [rang]- future [ring]), and their relatedness to action, we can find it is a topic already discussed in the field of Artificial Intelligence... because electrical conductivity is its own language.
Conjugating verbs In one famous connectionist experiment conducted at the University of California at San Diego (published in 1986), David Rumelhart and James McClelland trained a network of 920 artificial neurons, arranged in two layers of 460 neurons, to form the past tenses of English verbs. Root forms of verbs—such as come, look, and sleep—were presented to one layer of neurons, the input layer. A supervisory computer program observed the difference between the actual response at the layer of output neurons and the desired response—came, say—and then mechanically adjusted the connections throughout the network in accordance with the procedure described above to give the network a slight push in the direction of the correct response. About 400 different verbs were presented one by one to the network, and the connections were adjusted after each presentation. This whole procedure was repeated about 200 times using the same verbs, after which the network could correctly form the past tense of many unfamiliar verbs as well as of the original verbs. For example, when presented for the first time with guard, the network responded guarded; with weep, wept; with cling, clung; and with drip, dripped (complete with double p). This is a striking example of learning involving generalization. (Sometimes, though, the peculiarities of English were too much for the network, and it formed squawked from squat, shipped from shape, and membled from mail.) Another name for connectionism is parallel distributed processing, which emphasizes two important features. First, a large number of relatively simple processors—the neurons—operate in parallel. Second, neural networks store information in a distributed fashion, with each individual connection participating in the storage of many different items of information. The know-how that enabled the past-tense network to form wept from weep, for example, was not stored in one specific location in the network but was spread throughout the entire pattern of connection weights that was forged during training. The human brain also appears to store information in a distributed fashion, and connectionist research is contributing to attempts to understand how it does so. B.J. CopelandSource: "Artificial Intelligence (AI) ." Encyclopædia Britannica Ultimate Reference Suite, 2013. |
But connectionist approaches have themselves been directed along a binary orientation of externalized real world approaches versus internalized symbolic realities for developing relativistic AI models... though both are actually constituents of the same overall desire. They are merely different approaches to the same problem. Instead of creating an internalized symbolic world, externalized "real world" approaches frequently create artificial environments thought to be close approximations to reality... which, in a sense, is the creation of a "symbolic" external reality. Thus, we have the binary situation of one creating an external "symbolic" environment and another creating an internal "symbolic" environment, with the words "environment" and "reality" being used inter-changeably.
The approach now known as nouvelle AI was pioneered at the MIT AI Laboratory by the Australian Rodney Brooks during the latter half of the 1980s. Nouvelle AI distances itself from strong AI, with its emphasis on human-level performance, in favour of the relatively modest aim of insect-level performance. At a very fundamental level, nouvelle AI rejects symbolic AI's reliance upon constructing internal models of reality... Practitioners of nouvelle AI assert that true intelligence involves the ability to function in a real-world environment. A central idea of nouvelle AI is that intelligence, as expressed by complex behaviour, “emerges” from the interaction of a few simple behaviours. For example, a robot whose simple behaviours include collision avoidance and motion toward a moving object will appear to stalk the object, pausing whenever it gets too close. Nouvelle systems do not contain a complicated symbolic model of their environment. Instead, information is left “out in the world” until such time as the system needs it. A nouvelle system refers continuously to its sensors rather than to an internal model of the world: it “reads off” the external world whatever information it needs at precisely the time it needs it. (As Brooks insisted, the world is its own best model—always exactly up-to-date and complete in every detail.) B.J. CopelandSource: "Artificial Intelligence (AI) ." Encyclopædia Britannica Ultimate Reference Suite, 2013. |
Impulse response An optical system that employs incoherent illumination of the object can usually be regarded as a linear system in intensity. A system is linear if the addition of inputs produces an addition of corresponding outputs. For ease of analysis, systems are often considered stationary (or invariant). This property implies that if the location of the input is changed, then the only effect is to change the location of the output but not its actual distribution. With these concepts it is then only necessary to find an expression for the image of a point input to develop a theory of image formation. The intensity distribution in the image of a point object can be determined by solving the equation relating to the diffraction of light as it propagates from the point object to the lens, through the lens, and then finally to the image plane. The result of this process is that the image intensity is the intensity in the Fraunhofer diffraction pattern of the lens aperture function (that is, the square of the Fourier transform of the lens aperture function; a Fourier transform is an integral equation involving periodic components). This intensity distribution is the intensity impulse response (sometimes called point spread function) of the optical system and fully characterizes that optical system. With the knowledge of the impulse response, the image of a known object intensity distribution can be calculated. If the object consists of two points, then in the image plane the intensity impulse response function must be located at the image points and then a sum of these intensity distributions made. The sum is the final image intensity. If the two points are closer together than the half width of the impulse response, they will not be resolved. For an object consisting of an array of isolated points, a similar procedure is followed—each impulse response is, of course, multiplied by a constant equal to the value of the intensity of the appropriate point object. Normally, an object will consist of a continuous distribution of intensity, and, instead of a simple sum, a convolution integral results. Source: "Optics." Encyclopædia Britannica Ultimate Reference Suite, 2013. |
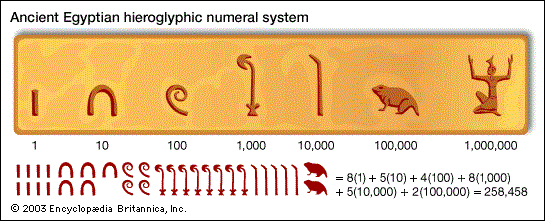
The usage of a binary system was developed from an analog(y) perspective that was applied to a digital representation that was adapted to an on/off electrical situation. Making the comparisons that I am, is the usage of an analog formula. It requires a flexibility in generalization that can be scrutinized into a specificity to which number values can be applied. The usage of zeros and ones in a binary computer environment is not a true counting system. It is a system of association that does not actually utilized quantity as a means of referencing a value. The usage of a zero and a one are pictographs... like the hieroglyphics of ancient civilizations.
 |
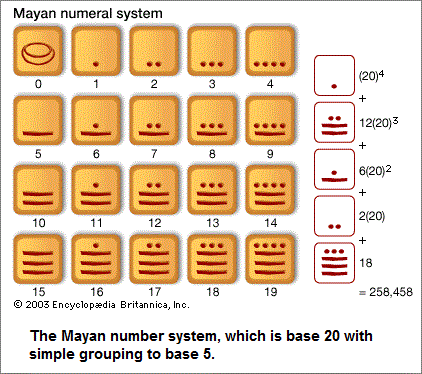 |
Like the development of writing, and in particular, the numerical short-hand notes used for business calculations and transaction, there is efficiency and economy (conservation of effort) in writing and using a binary system. However, as a language, though the numerical indices of zero and one are used as a hieroglyphic-like short-hand notation, the usage of trilingual inscriptions have assisted us in developing a clearer grasp of ancient texts. Yet, the primivity of the texts as portrayals of ideas, do not express the complexity of thoughts which no doubt exceeded the means by which they were conveyed. Because writing was at a primitive stage of development, we might want to assume that complex thoughts could not be adequately articulated. A binary system is likewise a primitive language and needs to be upgraded to a "trilingual" transcription.
Here are 3 examples of trilingual inscriptions followed by a Britannica article revealing a recurrence of a "three" formula:

Engraved on a cliff ledge 345 feet about the ground, the Behistun Inscription stands as a monumental feat of the ancient world. Located at the foot of the Zagros Mountains in western Iran near the modern town of Bisitun, the Behistun Rock was commissioned by King Darius I of Persia (522 - 486 B.C.).
King Darius I of Persia had it cut in the rock at the time of one of his great military victories. It includes a large panel which depicts the scene of his victory, and then three panels underneath with the text. Each panel is in a different language: Old Persian, Akkadian (or Babylonian), and Elamite. (H.O.B. note: The three languages are sometimes given as Old Persian, Assyrian and Susian.)
Behistun Rock information sources:
The Behistun Inscription by Jona LenderingBehistun Rock
Truth Magazine.com archives (The Rosetta Stone and the Behistun Rock by Joe R. Price)

The Galle Trilingual Inscription is a stone tablet inscription in three languages, Chinese, Tamil and Persian, that was erected in 1409 in Galle, Sri Lanka to commemorate the second visit to the island by the Chinese admiral Zheng He. The text concerns offerings made by him and others to the Buddhist temple on Adams Peak, a Mountain in Sri Lanka, Allah (the Muslim term for God) and the god of the Tamil people, Tenavarai Nayanar. The admiral invoked the blessings of Hindu deities here for a peaceful world built on trade. The stele was discovered in Galle in 1911 and is now preserved in the Colombo National Museum.
Galle Inscription information source:
Wikipedia: Galle
Trilingual Inscription

(Is an)ancient Egyptian stone bearing inscriptions in several languages and scripts; their decipherment led to the understanding of hieroglyphic writing. An irregularly shaped stone of black granite 3 feet 9 inches (114 cm) long and 2 feet 4.5 inches (72 cm) wide, and broken in antiquity, it was found near the town of Rosetta (Rashi-d), about 35 miles (56 km) northeast of Alexandria. It was discovered by a Frenchman named Bouchard or Boussard in August 1799. After the French surrender of Egypt in 1801, it passed into British hands and is now in the British Museum in London.
The inscriptions, apparently composed by the priests of Memphis, summarize benefactions conferred by Ptolemy V Epiphanes (205–180 BC) and were written in the ninth year of his reign in commemoration of his accession to the throne. Inscribed in two languages, Egyptian and Greek, and three writing systems, hieroglyphics, demotic script (a cursive form of Egyptian hieroglyphics), and the Greek alphabet, it provided a key to the translation of Egyptian hieroglyphic writing.
Rosetta Stone information source: "Rosetta Stone." Encyclopædia Britannica Ultimate Reference Suite, 2013.
(The name "Rosetta Stone" is now frequently applied to just about any type of key used to unlock a mystery.)With respect to three-language inscriptions, the following article depicts a frequent usage in several nation states; no doubt because the populations which inhabited them were multi-lingual. Nonetheless, the usage of "three" instead of some other quantity (such as two) should be noted. Though there may have been many individuals who spoke two languages, authority used three as a type of universal application. So did biology in terms of a triplet coding system in DNA.
|
Decipherment of cuneiform Many of the cultures employing cuneiform (Hurrian, Hittite, Urartian) disappeared one by one, and their written records fell into oblivion. The same fate overtook cuneiform generally with astonishing swiftness and completeness. One of the reasons was the victorious progress of the Phoenician script in the western sections of the Middle East and the Classical lands in Mediterranean Europe. To this writing system of superior efficiency and economy, cuneiform could not offer serious competition. Its international prestige of the 2nd millennium had been exhausted by 500 BCE, and Mesopotamia had become a Persian dependency. Late Babylonian and Assyrian were little but moribund artificial literary idioms. So complete was the disappearance of cuneiform that the Classical Greeks were practically unaware of its existence, except for the widely traveled Herodotus, who in passing mentions Assyria Grammata (“Assyrian characters”). Old Persian and ElamiteThe rediscovery of the materials and the reconquest of the recondite scripts and languages have been the achievements of modern times. Paradoxically the process began with the last secondary offshoot of cuneiform proper, the inscriptions of the Achaemenid kings (6th to 4th centuries BCE) of Persia. This is understandable, because almost only among the Persians was cuneiform used primarily for monumental writing, and the remains (such as rock carvings) were in many cases readily accessible. Scattered examples of Old Persian inscriptions were reported back to Europe by western travelers in Persia since the 17th century, and the name cuneiform was first applied to the script by Engelbert Kämpfer (c. 1700). During the 18th century many new inscriptions were reported; especially important were those copied by Carsten Niebuhr at the old capital Persepolis. It was recognized that the typical royal inscriptions contained three different scripts, a simple type with about 40 different signs and two others with considerably greater variations. The first was likely to reflect an alphabet, while the others seemed to be syllabaries or word writings. Assuming identical contents in three different languages, scholars argued on historical grounds that those trilingual inscriptions belonged to the Achaemenid kings and that the first writing represented the Old Persian language, which would be closely related to Avestan and Sanskrit. The recognition of a diagonal wedge as word-divider simplified the segmentation of the written sequences. The German scholar Georg Friedrich Grotefend in 1802 reasoned that the introductory lines of the text were likely to contain the name, titles, and genealogy of the ruler, the pattern for which was known from later Middle Iranian inscriptions in an adapted Aramaic (i.e., ultimately Phoenician) alphabet. From such beginnings, he was eventually able to read several long proper names and to determine a number of sound values. The initial results of Grotefend were expanded and refined by other scholars. Next the second script of the trilinguals was attacked. It contained more than 100 different signs and was thus likely to be a syllabary. Mainly by applying the sound values of the Old Persian proper names to appropriate correspondences, a number of signs were gradually determined and some insight gained into the language itself, which is New Elamite; the study of it has been rather stagnant, and considerable obscurity persists. The same holds true for the Old Elamite of the late 2nd millennium. Akkadian and SumerianThe third script of the Achaemenian trilinguals had in the meantime been identified with that of the texts found in very large numbers in Mesopotamia, which obviously contained the central language of cuneiform culture, namely Akkadian. Here also the proper names provided the first concrete clues for a decipherment, but the extreme variety of signs and the peculiar complications of the system raised difficulties which for a time seemed insurmountable. The serious external divergencies between older and newer types of Akkadian cuneiform, the distribution of ideographic and syllabic uses of the signs, the simple (ba, ab) and complex (bat) values of the syllables, and especially the bewildering polyphony of many notations were only gradually surmised by scholars. Once the Semitic character of the language had been established, the philological science of Assyriology developed rapidly from the closing decades of the 19th century onward, especially because of scholars like Friedrich Delitzsch and, later, Benno Landsberger and Wolfram von Soden. Once Akkadian had been deciphered, the very core of the system was intelligible, and the prototype was provided for the interpretation of other languages in cuneiform. Until the 20th century Sumerian was not definitely recognized as a separate language at all but rather as a special way of noting Akkadian. Even when its independent character was established, the difficulties of interpretation were appalling because of its strange and unrelated structure. After Sumerian finally died out as a living language toward the middle of the 2nd millennium, it lingered on as a cult idiom of Babylonian religion. To facilitate its artificial acquisition by the priesthood, grammatical lists and vocabularies were compiled and numerous religious texts were provided with literal translations into Babylonian. These have facilitated the penetration of unilingual Sumerian texts, and Sumerian studies advanced greatly through the efforts of such scholars as Delitzsch, François Thureau-Dangin, Arno Poebel, Anton Deimel, and Adam Falkenstein. Source: "Cuneiform." Encyclopædia Britannica Ultimate Reference Suite, 2013. |

The binary code used for computers based on the convention of an ON/OFF electrical switch... thus making a computer a box of small electrical switches taking place at a high rate of speed; is best described as a primitive hieroglyphic writing system. It is like a primitive mind cataloging a daily event in terms of light and darkness, though they are surrounded by biological activity taking place in response to three "moments" of the Sun referred to as Dawn- Noon- Dusk. The primitive mind did not perceive the impressions these three events created and were expressed with behaviors that are today overlooked by many people. The occurrence of (1) light and warmth after darkness and coolness, (2) the increase in intensity during the day and is sometimes denoted by hours one should not expose themselves to the sun for extended periods without sunblock, and (3) the forthcoming of darkness and diminishment of night... are types of behavioral switches. Depending on the physiology of a given life form, each responds to these events accordingly. However, are these switches taking place as an analog or digital communication? With Night and Day as a binary generalization, how should we characterize the three-moments influence?

Granted that the three-moment solar event is a pictograph, it is but one type of analogy being made in our search for a better model from which we might derive an enhanced form of computer code basis. The binary code is a linear formula that traces out linear forms of other geometric models, but can not achieve a three-dimensional portraiture. For example, if we try to use a binary code to draw a circle, we end up with a square, or having to use numerous inter-locked sequences to build the apparent design of a circle by way of multiple executions of "squaring the circle" over and over again so that the image of a circle is built by accumulations of linear events. Yet the circle which is seen on a flat surface does not achieve the dimension of a sphere. Likewise for a triangular image.
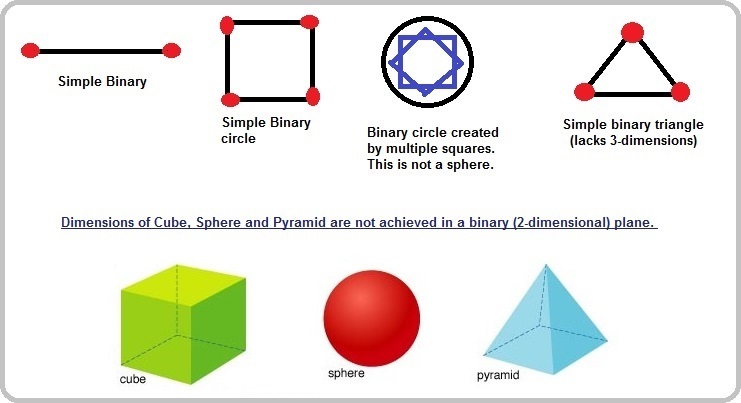
And though multiple trinary examples can be pointed out, we are still subjected to the functionality of a linear binary electrical circuit. Whereas attempts to go beyond this have and are being tried, we still witness an inclination to use a binary formula. One of the models being used has a biological background called DNA computing:
Form of computing in which DNA molecules are used instead of digital logic circuits. The biological cell is regarded as an entity that resembles a sophisticated computer. The four amino acid bases that are constituents of DNA, traditionally represented by the letters A, T, C, and G, are used as operators, as the binary digits 0 and 1 are used in computers. DNA molecules are encoded to a researcher's specifications and then induced to recombine (see recombination), resulting in trillions of “calculations” simultaneously. The field is in its infancy and its implications are only beginning to be explored. Source: "DNA computing." Encyclopædia Britannica Ultimate Reference Suite, 2013. |
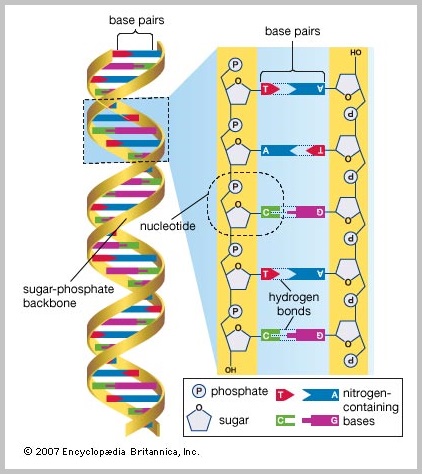
The DNA strand thus becomes the model upon which a computational formula is derived. Unfortunately, the pairing of amino acids is used as a substitute type of binary formula. The rest of the DNA strand is likewise viewed from a binary perspective. Such a perspective does not take the whole population of the macromolecular (super-molecular) domain into consideration as part of the formula. For example, the 1, 2, 3 strands of DNA and RNA are not contrasted with the primary, secondary, tertiary structure of Proteins, nor the inclusion of the quaternary structure as part of a 3 to 1 ratio. In addition, the realization that the helical structure makes one complete turn approximately every 10 base pairs may or may not be correlated to a base 10 numbering system. In short, while a biological model is viewed as a possible diagram exceeding current binary formulas, a binary formula is often used in a particular way corresponding to a biological model. It's like substituting a preoccupation with a swing in motion for that of the motion viewed in a see saw... though both have a binary element.
Subject page first Originated (saved into a folder): Thursday, November 13, 2014... 5:50 AM
Page re-Originated: Sunday, 24-Jan-2016... 08:51 AM
Initial Posting: Saturday, 13-Feb-2016... 10:59 AM
Updated Posting: Sunday, 23-June-2019... 2:46 PM
Herb O. Buckland
herbobuckland@hotmail.com