(Static -vrs- Dynamic)
2
~ The Study of Threes ~
http://threesology.org
Visitors as of 2/27/2021

In looking at the various three-patterned examples, some of you may have realized you are looking at proportionalities, and this is exactly what mathematics equations present us with... different proportionalities. However, typically, proportionality is thought of in terms of direct proportionality and Inverse proportionality. In direct proportionality, you get paid a certain amount of money per hour and will receive that amount for each hour you work. Half an hour's worth of work will get you half your wage for that period of time. In direct proportionality you discover which is constant, the money or the time. It is the wage which remains constant because you may not always work the same amount of time. You adjust the amount you earned by the constant of your wage and the time you worked. Many workers use proportionality often in a rough calculation approach in their head to figure out about how much they'll earn by working a certain number of hours. Then the local, state and federal governments (in the United States) removes their tax deduction constants before you get your pay check, unless you mess around with how many deductions you are claiming in order to get more or less money per pay check, which then alters how much or how little you will get back from a tax return. In Inverse proportionality one side of one's personal financial equation (such as balancing a check book) goes up (more) while the other side goes down (less). This type of proportionality is akin to the double-entry book keeping method that can be simplified by calling it a pattern of two.
With respect to proportionality and patterns-of-three (though other types of enumerated proportionalities can have more-than-three divisions), we can use gunpowder for example:
Rather than being one particular compound, gunpowder is actually a mix of three different components. It consists of potassium nitrate (75% by weight), charcoal (10% by weight), and sulfur (5% by weight). Each of these components plays an important role in the combustion of gunpowder. (How Gunpowder makes explosions by Leslie Baehr , Compound Interest; Jul 9, 2014, 8:48 AM)
...it has become customary to view mathematical research as establishing truth by rigorous deduction from appropriately chosen axioms and definitions. Wikipedia: Mathematics
Explanation of Axioms "7 (plus or minus) 2" (unless one prefers 5 + 2 + 2; or 9 -2 -4): (And no, I did not miss the correlation between George A. Miller's paper entitled The Magical Number Seven, Plus or Minus Two: Some Limits on Our Capacity for Processing Information).
- Five Axioms of Algebra: AAA Math: Basic Axioms of Math
- Seven Axioms of Euclid: Introduction To Euclidean Geometry
- Nine set theory Axioms of Zermelo-Fraenkel (ZF) Axioms and Proof
Mathematicians assume that axioms are true without being able to prove them. However this is not as problematic as it may seem, because axioms are either definitions or clearly obvious, and there are only very few axioms.... Proofs are what make mathematics different from all other sciences, because once we have proven something we are absolutely certain that it is and will always be true. It is not just a theory that fits our observations and may be replaced by a better theory in the future... Many mathematical problems can be formulated in the language of set theory, and to prove them we need set theory axioms. Over time, mathematicians have used various different collections of axioms, the most widely accepted being nine Zermelo-Fraenkel (ZF) axioms. (Axioms and Proof)
... calculus has no axioms inherent to itself. Theorems of calculus derive from the axioms of the real, rational, integer, and natural number systems, as well as set theory. Problems with Axioms
These are the nine (sometime ten) axioms:
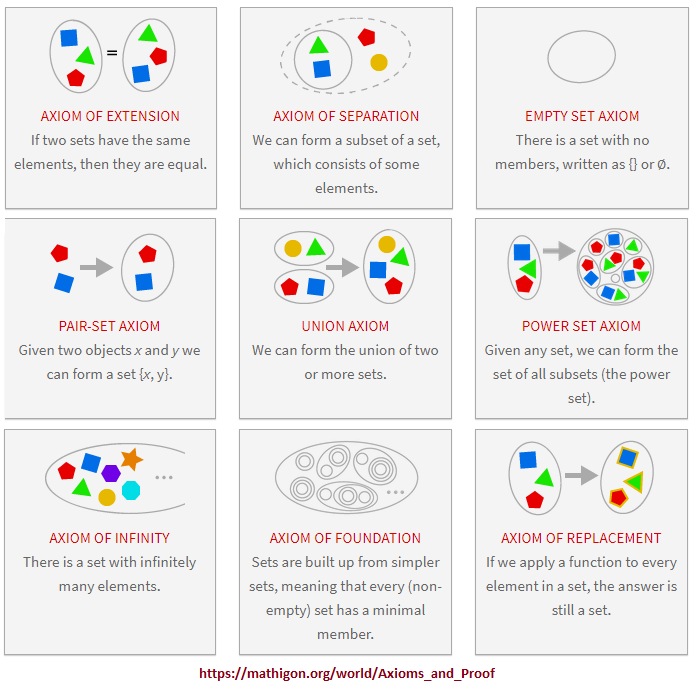

With respect to calculus, it is sometimes said that there are two basic concepts (or fundamental ideas) one needs to know: (derivative and integral); and then there are those who prefer to say: he Three Calculus Concepts You Need to Know
- Limits predict the value of a function at given point.
- Derivatives give the rate of change of a function.
- Integrals calculate area, and they are the opposite of derivatives.
The two versus three cognitive orientation is quite old, as can be seen in the following image:
 |
Roman dicers from a fresco at Pompeii, playing what is thought to be an early version of backgammon. The cartoon-like captions above their heads describe a disputed call: the man on the left cries, "i've won!" while the one on the right objects, claiming, "It's not a three, it's a two." Analogously, the two characters can be viewed as the right & left hemispheres of the Triune brain The right adamantly refuses to acknowledge the left's claim to a 3 and insists that the "3" the left sees is actually a 2. if the overall purpose of the "game" (life) is to achieve a "3" and yet there is a claim from some for a preponderance of "2" (with all its various guises), do we try to change the rules of the "game" or create a teaching methodology which enables the distinctions of "2" and "3" to be made identifiable and useful from all vantage points? (even if the purpose of the game is defined by earth-specific environmental circumstances.) the social problems created by an underlying 2 versus 3 contention has been going on for long enough... since pompeii anyway. let's not leave a similar picture of us for future historians who find it beneath the rubble of an extinct civilization. |
Despite the usage of axioms, we can quantify a difference of cognitive orientation amongst those involved in computations. In short, if mathematicians are not aware of this inclination, then they can not be aware of how they might beneficially use the different orientations in acquiring a new perspective... not only of calculus, but other maths as well? In other words, if a person's mind is predominantly using an underlying two-patterned organizational formula, conflicts might well necessarily arise with those who use a predominant three-patterned orientation... not to mention the underlying pattern upon which calculus and the other maths are architectured. 3's poster column 8.
From a different perspective, if we ask a dog to proof an aspect of reality they will most likely use the methodology of scent. A spider may use vibrations on its web. No less, some humans smell their food as a "proofing" measure, while others look at texture and color and still others need to touch and listen to an item... such as for example, a watermelon. At one time it was common practice for a produce man to "pull a plug" (cut out a small triangular portion) in order for a prospective customer to taste what they are thinking of buying. This of course was during an era when the cost of a watermelon was a nickel a pound or less.
Despite all the standardization of proofs, of what value are they if we have people whose underlying cognitive preference differs from the underlying schematic upon which a math was designed? If we have a mathematician whose preference is to use some abstractionated method for smell, or sound, or sight, or touch, or taste projected onto their mathematical behavior, then we have undisclosed methods of proofing that are not being taken into account. In other words, calculus and the other maths are stifled in their ability to mature beyond where they are now. Far too many people think that the mathematics which they do day in and day out, "is what it is", as the colloquial expression goes when shrugging one's shoulders in deference to the way things appear to be as dictated by tradition. Like primitive people who initially stopped counting at the number one, larger numbers were not even being considered. Until of course the mind of humans began to emerge towards some semblance of a number maturity where they then identified some language equivalent model to express a "2" quantity ... until yet another stopping point arose to rein in further steps. After which, when the next quantity was initially recognized as much, many, more or whatever word was used to describe some quantity beyond the contemporary stopping point but still speak of the metaphysical idea of the "else" or "other" beyond conventional appreciations; such examples speak of present maths as small number concept equivalents. We are using calculus as if to express some primitive's illustration of all quantities beyond two described as "Many". In the movie The Clan of the Cave Bear, a young Cro-Magnon girl is adopted into a Neanderthal clan, despite opposition. Differences in cognitive behavior become highlighted, even to the extent that she (Ayla) can count higher than the others, and is cautioned not to let anyone know she has this ability because it will upset the status quo thinking.
Ayla's different thought processes lead her to break important Clan customs, particularly the taboo against females handling weapons. She is self-willed and spirited, but tries hard to fit in with the Neanderthal's, although she has to learn everything first-hand; she does not possess the ancestral memories of the Clan which enable them to do certain tasks after being shown only once.

The art of counting in the Clan of the Cave bear
The point I am trying to make is that differences in thought processing are not being permitted to emerge by current practices of mathematics. You are forced to toe-the-line... even if you want to swing from and to different heights, you must do so within the limits of the current forms of mathematical rock climbing (so to speak); where ropes are said to be used only for safety, but are in fact types of chemical restraints. Whereas this analogy can be misread because metaphors carried too far often admit to fallacies, as an analogy to perceived constraints, it is useful. The problem is the restraints are said to be necessary, only because the same sorts of rocks are being surveyed to be climbed again and again by each generation of students being subjected to the indoctrination of mathematics that is being drilled into them as an attempt to establish an addictive process that everyone in society is habituated to. While the same is true for the sales of coffee and tobacco and many other products such as the lottery, social security, military conscription (if necessary), pathetically run small claims courts process, the S.E.C. and its hired guns, and a host of other currencies of practiced Neanderthal-like orientations; mathematics should have the perspicuity to step beyond it preset formula of swinging from tree to tree like Tarzan and cheetah.
But how does one go about describing a Cro-magnon level of conception if mathematics was designed from Neanderthal brains that all of society has bought into because it has been applied like an addictive drug that no one chose, but were forced to adopt as a primary thinking pattern and tool for conceptualizing a world whose reality is based upon the same perceptual peculiarities? Basically, speaking in retrospect, climbing is carried out with or without ropes, where alternative types of hand-holds (tree limbs, boulders, clefts in stone, shrubbery, or some sharp tool to dig into the surface), are utilized. Here we return to the "two" orientation found also in the binary code of computers where a three-patterned boolean logic is applied, and futuristic thinkers are trying to develop a ternary computer profile based on some quantum scaffolding. If one wants, they can find articles on two types of rock climbing, three forms of rock climbing and many types of rock climbing; all of which have an expressed conservation, depending on whether one is speaking with an amateur rock climber, a professional rock climber, or a business oriented towards teaching whichever brand of rock climbing will net them a profit. The "many" approach is the scavenger or generalist approach, whereas a beginner or professional may focus on one or two or three types which they are most interested in and/or familiar with enough to speak intelligently about. Specific types of rock climbing may be broken down into enumerated categories representing their own forms of conservation... or the "limit" designation if one is in the habit of visually translating written and/or spoken speech into equations, diagrams, geometries, musical score, artistic dimensionality, etc..
Boolean algebra or logic: a type of algebra which can be applied to the solution of logical problems and mathematical functions, in which the variables are logical rather than numerical, and in which the only operators are AND, OR and NOT. Glossary of Mathematical terms and Definitions
Most disciplines of modern mathematics exhibit this sort of behavior, in which the discipline has no axioms inherent to itself. Modern disciplines of mathematics typically work under a unified axiomatic system, the most common one being Zermelo-Fraenkel set theory with the Axiom of Choice (ZFC). ZFC is powerful enough to encode our most frequently encountered structures, including our various number systems... ( Problems with axioms by Gyu Eun Lee)
The reference "Accordian Calculus" is being used to describe equations that have motion, and to be distinguished from the purported motion illustrated in kinematic equations. However, let it be fully understood that while there is a corpus of activity designated as Infinitesimal Calculus, there is not a presently designated area of mathematical study explicitly referred to as "Accordian Calculus". The phrase is my attribution for a currency of thought I shall attempt to convey from a variety of perspectives which I believe has merit for consideration and further development. Like Sir Isacc Newton's development of Three laws of Motion and Johannes Kepler's Three laws of planetary motion I see a repetition of three which needs to be examined as to its cognitive implications on our mathematics and other inquiries of reality, such as this attempt: Examining the Triple Code Model in numerical cognition: An fMRI study by Mikael Skagenholt, Ulf Träff, Daniel Västfjäll, Kenny Skagerlund; Published: June 28, 2018.
Newton's 3 laws of motion:
- Every object in a state of uniform motion will remain in that state of motion unless an external force acts on it.
- Force equals mass times acceleration [ f(t)= ma(t) ].
- For every action there is an equal and opposite reaction.
The first law, also called the law of inertia, was pioneered by Galileo. This was quite a conceptual leap because it was not possible in Galileo's time to observe a moving object without at least some frictional forces dragging against the motion. In fact, for over a thousand years before Galileo, educated individuals believed Aristotle's formulation that, wherever there is motion, there is an external force producing that motion.
The second law, f(t)= ma(t), actually implies the first law, since when f(t)= 0 (no applied force), the acceleration a(t) is zero, implying a constant velocity v(t). (The velocity is simply the integral with respect to time of a(t)={\dot v}(t).)
Newton's third law implies conservation of momentum. It can also be seen as following from the second law: When one object "pushes" a second object at some (massless) point of contact using an applied force, there must be an equal and opposite force from the second object that cancels the applied force. Otherwise, there would be a nonzero net force on a massless point which, by the second law, would accelerate the point of contact by an infinite amount.
In summary, Newton's laws boil down to f= ma. An enormous quantity of physical science has been developed by applying this simpleB.1 mathematical law to different physical situations.
Kepler's 3 laws of planetary motion:
- Every planet's orbit is an ellipse with the Sun at a focus.
- A line joining the Sun and a planet sweeps out equal areas in equal times.
- The square of a planet's orbital period is proportional to the cube of the semi-major axis of its orbit. As it's the third which is most often used, Kepler's law usually means Kepler's third law (of planetary motion).
Before one goes about developing a new form of Mathematics, there is an interval where it is preceded by a philosophy enabling for such a realization to emerge from the recesses of one's collectivity. Let us begin this Accordian Calculus...

Unfortunately, in beginning our sojourn, we are confronted by an unexpected crossroads. While the school of peripatetic walkers with staff in hand might well have given us a heads-up, we have been led to believe by preoccupations of over-indulging in inspirational meanderings, to expect a milestone... a sign in a single road to accomplishing what appears at first to be such a simply task because truth is truth and it is an axiom that is easily recognized and understood; we find that in our attempts to get the simplest of directions from the wisest of mathematical and philosophical counsels, we come to appreciate there is a vast language difference. While so many of us fully realize the difficulty in birds talking to squirrels and that while there is no communication among ants an termites there can exist a symbiotic relationship, one might well expect humans to find some common ground. However, this is not the case. Addicted people are sometimes flying so high they think of themselves as butterflies and all others are caterpillars. It much like trying to find a means by which one can learn how to communicate with a kite... one must first come to grips with the fact that there are many types of kites and that they all fly at different heights.
Indeed, restated from the backdrop of the previous commentary... the problem is, however, that in proposing a different orientation for mathematicians, one is confronted by the realization that Mathematics is an addiction for many practitioners. Just like religion, or sports, and numerous other activities. This being the case, should one use the drug(s) of a specific addiction like mathematics to get mathematic addicts off their drug-of-choice, only to get them hooked onto another type of drug that they are unaccustomed to and can not readily see any fortuitous benefits that are presently being acquired by the usage of their present preference? The situation is like gathering a bunch of addicts into a program that is meant to get them off of an addiction, yet carry out group sessions in which the members of the group get high off of one-another's drug usage experiences. Whereby instead of paying a drug dealer for a drugged experience, one now pays an anti-drug dealer who doesn't actually want to cure anyone completely, because their livelihood is dependent on a continuous line-up of customers to their doors, which are not always recognized as being revolving ones.
The larger situation involving the presentation of a new direction in mathematics to be undertaken, is that current drug dealers such as Universities, like the supply and demand created by an adopted addiction begun in elementary school. They simply capitalize on the previous (required course of) doses by offering forms of mathematics which are labeled as "Higher" models of intellectual enterprising. Our entire civilization has bought into this drug trade of mathematics intoxication, despite the fact that it rests on beliefs and assumptions transmutated into the sum called Axiom. It is religion in another guise, having its own forms of golden fleece, golden chalice and routing the dragon to win the fair maiden's hand who bears the title of being a princess, as icing on the academic achievement cake. Unless of course one is a female mathematician whose exercises of mathematical dexterity can win her a coveted prize worthy of her gender and respective honors of being knighted and accepted at some geometrically designed table to give the impression of equality... as King Arthur's supposedly did by using a round table for his knights that were nonetheless sworn to uphold the standards set forth by the King and his ulterior motivated advisers.
So what does one do? Do we effect some sort of scenario to create a cold-turkey situation where the screams, condemnations, cajoling, promises, lies, and so forth spew out against such an act that is meant to be well-meaning but will likely resort in vituperations in accord with one's type and level of venom may be unleased from their fangs of self-defense for upholding the faith of their profession in which they may have well climbed the circular stairway to achieve dazzling mathematical views from unimagined heights accessed by tenured mental activity like a faithful slave given some concessions by developing a keen mastery of a given craft of activity? Is there one particular or many particular mathematicians whom we should kidnap and subject to a cold-turkey setting as a means to create a wedge to be used in asserting our views against the whole entire global community of mathematicians in their respective clans using the preferred language of their intellectual genres? Or must we, with an unparalleled foresight choose instead to speak up and out as did Socrates and no doubt many others who were faced with a system of gamed jurisprudence so very evident today in all governments, businesses and religious 'circles' as well. What then will be our final word before the guillotine of practiced mathematical ideology glistens its angled and frothing tooth at the prospect of defending its self-proclaimed righteousness by simply dismissing alternative exercises of thought by claiming them to be uncouth vagrancies which nuance themselves as a perceive nuisance to the more refined ideological pretensions mathematics claims for itself?
Is there to be not better course for relieving such an addiction than to resort to some antiquated theological or philosophical concoction that will enable these institutions to once again arise to a preferred station of exultation that its practitioners think is deserving and foremost enviable? Is a recurring charlatanism the only viable alternative to such a widespread addiction as mathematics training and expectation? Is there no greater formula of thought to emerge from human consciousness than that which has not rescued humanity from economic travails, improvisation, war, blight, famine and many other tortures that the past itself had to endure? Whereas the beginnings of Sociology were preached by its originators as a better drug to be bathed in because it would thus reveal a grander world for all to live in by way of applying its model of mathematics towards solving social problems..., only to find that it too was a false hope that even now mathematics dares to claim it has no part in— and can thus wash its hands of all blood-stained exercises humanity has found itself in by using the geometricized contours of mathematics and religion and business and so very many political schemes advancing this cause, then another cause... all with some word coined from the womb of a greater ideal that has not been realized... and cannot be, because at the very least, there are three variables are being excluded from the equations being proposed by those advocating a different orientation is needed by all of humanity to embrace.
These three variables are the Sun's energy burning out, the Earth's rotation slowing, and the Moon receding. Three very simple variables that the current addictions of mathematics, religion, business, and government do not take into serious consideration, and therefore assign them with a stamp of negligibility to the point of irrelevance because they all too well exhibit these addictions as fallacies.
Calculus is suffocating. We need to either teach its practitioners to breathe more deeply, or we must resign ourselves to the appreciation that a new formula of mathematical inquiry must be architecturally asserted as when the usage of the wheel and fire had dawned; whether before or after human consciousness ascertained the realization of usefulness in order to explore creative forms of inventive computation thereof, from which numerous technologies and applications have arisen. The origination of the word "Calculus" either interpreted as a pebble or stone, lends itself to the usage of a metaphor in which calculus needs to be tossed into a pond (lake/ocean) of consideration in order to reverberate in those types of concentric circlings onto the many shores of analogized and metaphorised inclusions. In other words, the presentation of an idea such as "Accordian Calculus" requires the usage of multiple digressions for the purpose of making comparisons to reach different orientation of thought processing, in order that the utility of its next design embraces a variety of perspectives and their respective vantage points, accompanied by their own preferred language uses. Indeed, the language(s) of mathematics creates very many problems, despite the claim by an egotistical few who view it as such a remarkably basic representation of reality, that surely... all supposed sentient (intelligent) Alien others living in (outer) Space, will be able to readily communicate with humanity because humanity has achieved such an excellence of thought processing!
As such, Mathematics has not provided us with a clear-cut equation which quantifies human arrogance... unless that is what the infinity symbol actually stands for.
Date of Origination: 26 February 2021... 6:59 AM
Initial Posting:
June 3rd, 2021...7:56 AM