Threesology Research Journal

Mathematics Perspective: page 1

~ The Study of Threes ~
http://threesology.org

---

Visitors as of August 8th, 2022

Page 1	Page 2	Page 3	Page 4	Page 5
Page 6	Page 7	Page 8	Page 9	Page 10
Page 11	Page 12	Page 13	Page 14	Page 15
Page 16	Page 17

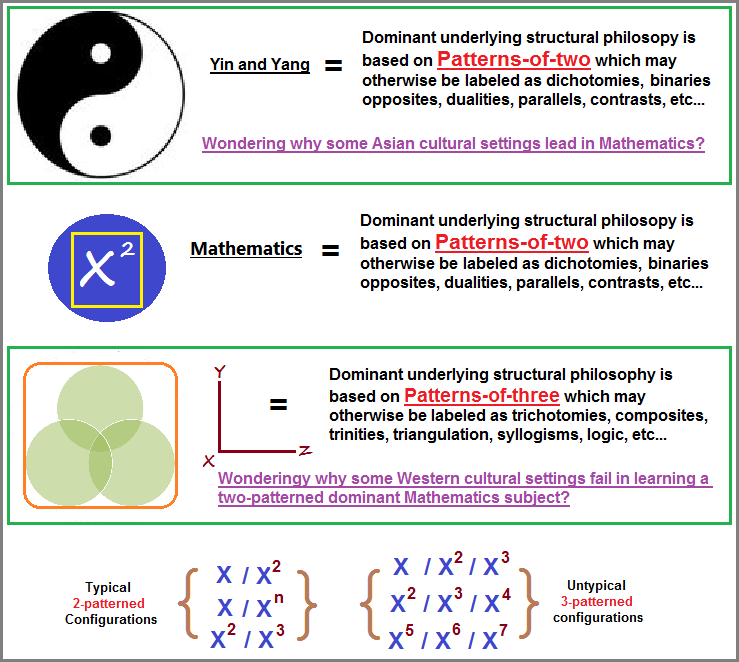
Entry: 2/2/2023:... As I glance back over this page seven months since it was first posted, and pay witness to some atrocious html errors, the central idea I wanted to convey at the time did not come forth as planned. The "Static versus Dynamic" equations concept resulted from visualization I kept having at the time, but owning to my rather poor skills at articulating ideas with equations, I chose to approach it from a philosophical perspective. In essence, I see Mathematics as a whole in a rather static mode of development, despite the use of equations to convey dynamic systems. I view this as being due to its origination from a later born, or let us say delayed development of Western thinking which had to play catch-up with the more Advanced intellectual development of the Chinese, who, in their own way centuries before and using their inclined artistically oriented tonal language (as opposed to the non-tonal mechanistically oriented Europeans); developed a methodological structural approach to understanding perceptions using a binary system widely known as the Yin and Yang. For whatever reason(s) the Indo-Europeans had a developmentally later start; and owing to much intellectual (exchange of ideas) isolation in centuries past, likewise followed a similar mental development utilizing a two-patterned structure which was first adopted by the then Philosophers, but was gradually overtaken and expanded on by Mathematicians. While it is not customary for the fundamental patterns of brain activity to be taught or studied (at least at that time from which the present day formula of teaching mathematics had been cemented into educational processes); it is not too difficult to see that Mathematics also has an underlying pattern-of-two structure, as represented by the following comparisons:

Persistent Dichotomies



The Psychological Scaffolding of Arithmetic
by Matt Grice, Simon Kemp, Nicola J. Morton, and Randolph C. Grace

Source: Mesologue

Mathematics is stuck in the Muck spinning its wheels giving the illusion it is dynamic. Much like those who are yearning for the development of a three-patterned (ternary/trinary) computer system to replace the current binary model, so too must humanity seek beyond its present model of Mathematics. While present mathematics is highly useful in the hands of practiced Mathematicians and everyday users of simply arithmetic, so too can be said for the use of crude tools used by a primitive person within the context of their social and environmental setting. And so long as the same social and environmental setting prevails, the tools and practitioners using those tools remain viably important, which may in part be why human society has not improved, because those in charge of society want to maintain a relative status quo for their own well-being, in which they have found a comfortable, if not lucrative niche.

One of the problems with those who have become adept at using Mathematics, much like an artist developing some command level of color and dimensional perspective along with brushes, canvas and the necessary politics of show and tell of their products, is that they are reliant upon an overall environmental system which they think is relatively stable, thereby ensuring a stability of the status quo for some time, at least their life time. However, the environment is changing and it appears that the human mind may be pursuing its own evolutionary - development if the idea of a ternary system of neuronal activity can be substantiated for some people. (Does the Brain Function as a Quantum Phase Computer Using Phase Ternary Computation? by Andrew S. Johnson and William Winlow:

)

Whereas the authors may be inclined to suggest such a state exists with everyone, this may not in fact be the case. It may be that such an activity is an internal expression of Evolution though most people are thinking in terms of some anatomical external change will come first. Whereas it is widely known that the size of a brain does not accurately describe intelligence, we must therefore consider the possibility that evolution may first (or separately) show itself by some internal brain modification, and with this an eventual alteration in ideas. There may be a distinction to be made that the authors have not considered with regard to their findings, such as the event being absent from some and more pronounced in others, and if found, would they be honest enough to tell the public.

he

The present multi-page essay uses basic numbers (0-1-2-3-4-5-6-7-8-9) to identify patterns being used in different subjects, sometimes by one or a few people, (or many thousands... as an expressed culturally embedded everyday exercise that may be taken for granted). Yet, while I do foray into multiple subjects to provide examples, the primary intent of the present extended essay is to show that current Mathematics primarily relies on the usage of dichotomies, in a similar fashion as one might find in the old yin/yang philosophy, which I believe is problematic if humanity wants to reach substantially beyond this two-patterned confinement and not merely by a superficial application of enlarged enumerations overlayed on these patterns-of-two such as in the case of using a three-based boolean Algebra applied to a two-based binary system seen in computer languages. This being said, it is of need to confront some eventual comments which arise concerning so-called "favorite" numbers used by different cultures that some viewers might interpret to mean there is no wide-spread discernible standard cognitive activity taking place with the present type of brain functioning evolution has provided humanity with.

Let me provide a few examples of dichotomies being used in mathematics and the reader will not react reflexively to the extent of putting up a defensively supportive explanation and leave themselves without some measure of open-mindedness.

• Rational/ Irrational numbers
• Positive/ Negative (yes, we can also add "neutral" to this ensemble as a third item)
• Odd/Even sequential counting
• Odd number only sequences (1,3,5...)/ Even number sequences only sequences (2,4, 6...)
• Upper case/ Lower case differentiations (Often seen in philosophy and genetics as intended Algebraic analogies: Pp, Aa, Cc, etc...)
• Subscript/ Superscript
• One side of an equation/ The other side of an equation
• Constant terms/ Variable terms
• Monomial equation (one term)/Polynomial equation (two or more terms)
• X and Y Coordinates
• Quality (Equal to)/ Inequality (less than/greater than)
• etc.

In at least one instance we see a duality in the form of pairing reflecting relative position of an observer, such as in the case of the two words Cardinality and Ordinality. Whereas Cardinality refers to a set of numbers, Ordinality refers to the order of the numbers within the set. We could also say that a set is derived from Ordinality, whether or not the order is of the 1-2-3... type, or a 1-3-5... sequence, or a 2-4-6... sequence. Whichever set one uses it can be described as a "Cardinal" set and the overall perspective of the set labeled an "Order". It is a duality some observers might prefer to refer to as a complimentary state of being, while others might be inclined to define them in terms of a separation based on a qualitative difference, and thus exert the notion of "difference" as an opposite, whether or not another observer calls this a prejudicial reading of the overall assigned contextual perception.

With respect to equations, some claim there are many kinds, while others lump them under Three Main Types of Equations:

1. Conditional Equations (Isolating variables to one side of a 2-sided equation)
2. Identity Equation (Both sides of equation are identical)
3. Formulas (Dependent/ Independent variables)

The point is, we can create cubic (3), quadratic (4), quintic (5)... etc. ideas using dichotomies as a base. We see an example of using the three basic gates (And, Or, Not) in computer languages where the underlying scaffolding is binary based on the on/off switching of an electrical circuit. (The Three Boolean Operators Example). The three AND- OR- NOT gates are overlays of the two ZERO- ONE identities substituting for the underlying OFF and ON switching character of electronic circuitry. And though Mathematics has ventured into using this same type of cognitive behavior with the usage of an obvious example such as Trigonometry. However, if we take the example of a three-variable equation in this "two- versus- three" illustration, we find that we are met with a behavior of eliminating one variable. Here is a reference to the idea:

Solving Systems of Three Equations in Three Variables

Source: https://math.libretexts.org/Bookshelves/Algebra/Map:_College_Algebra_(OpenStax)/07:_Systems_of_Equations_and_Inequalities/703:_Systems_of_Linear_ Equations_with_Three_Variables"

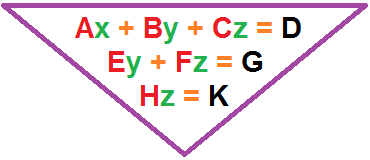
In order to solve systems of equations in three variables, known as three-by-three systems, the primary tool we will be using is called Gaussian elimination, named after the prolific German mathematician Karl Friedrich Gauss. While there is no definitive order in which operations are to be performed, there are specific guidelines as to what type of moves can be made. We may number the equations to keep track of the steps we apply. The goal is to eliminate one variable at a time to achieve upper triangular form, the ideal form for a three-by-three system because it allows for straightforward back-substitution to find a solution (x,y,z) , which we call an ordered triple. A system in upper (inverted) triangular form looks like the following:

Ax + By + Cz = D Ey + Fz = G Hz = K

While the elimination of one from a set of three may not readily be perceived as an apprehended usage of preserving a pattern-of-two, the uses of "two" in word form might be more enlightening for some when we take stock of Fairytales as representative word-problems; in that they are stories involving math requiring a solution. Instead of the positive/negative, real/imaginary, rational/irrational, whole/fraction (etc.) dichotomies seen in mathematics, we find the dichotomies of rich/poor, master/slave, strong/weak, good/evil, moral/immoral, etc... And while some who study literature view the presence of recurring numbers such as 3, 7, 9 (etc...) as conventions, the quantity of characters, character sets, or tasks to be performed, and incidentals which may change according to whom and when one gives a rendition of a given tale from memory, as apposed to reading an account which may itself exhibit altered variables analogously used as divisors, additions, subtractions, multipliers, exponents, fractions, etc... Whereas instructors may employ fairy tale themes in an effort to teach young children basic math concepts, Fairy tales themselves have (for the most part) been excluded from an examination of being scrutinized as being a differentiated cognitive expression of basic patterns which crop up in different subjects. In as much as they are simple patterns, so too are the patterns which we can find in any subject we look at. For example, despite the infinity of numbers both Nature and Humanity has at its disposal, only a very small (exceptionally conserved) quantity are being routinely used.

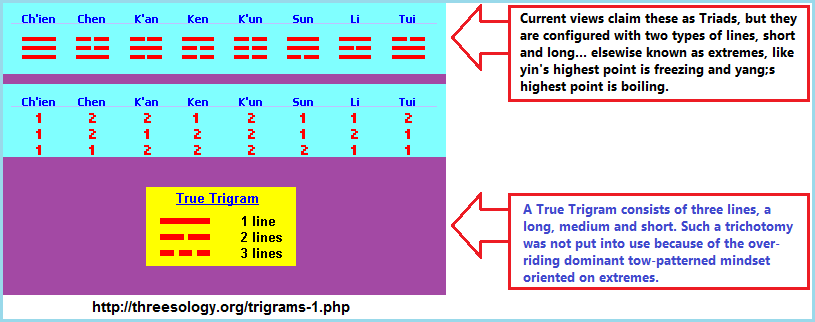
Another way of looking at the "2 versus 3" situation (noting that "versus" may be altered to words such as "and, but, or, minus, etc..."), is to look at the old two-patterned Yin/Yang idea coupled to what are described (in the I-Ching) as "Trigrams", but on closer examination are actually "Bigrams". To me it looks very much like the human mind in an ancient context is similar to that taking place in present day contexts where a "two" situation is over-lapped with a "three" designation in an effort to express some type of development beyond a "2" like primitive minds exerting an effort to exceed a count of "2" developed by way of pairing one item with another. Adding a third item, though it is constructed similarly to the former two items and naming it differently such as calling it a "three" (by way of a name such triad, trinity, triune, triple, triangle, treble, Trigram, etc...), a person can give themselves the impression of having reached beyond the conventional "two". This is not to say that such a perception will not create an intellectual environment from which a larger level of utilitarian models and ideas are proliferated, but that an actual "three state" has not been achieved. Only the desire by way of an adopted illusion out of which a reality is established in which others participate and refer to it as normal, natural, progressive, etc...

In the I-Ching, we find 8 sets of 3 line configurations referred to Trigrams. Let me provide three images displaying the same idea:

Persistent Dichotomies pg. 1

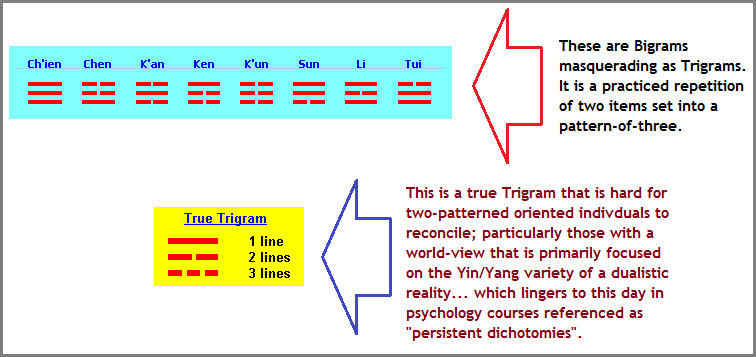
Information on Trigrams for those interested: Eight Trigrams by Michael P. Garofalo, © Green Way Research, Red Bluff, California, 2004-2020

It is known by those who research number references used in different cultures (such as research by cultural anthropologists), that different cultures apparently have an inclination to perceive and organize perceptions by way of a repetitive number value that outsiders may define as a culturally-defined favorite number, or sacred number, or a mythologically occurring repetition. Let us take for example the number three (since "three") forms the basis of the Threesology Research website, though a few other numbers could be used to highlight protracted and detracted examples of recurrence. (In other words, some numbers showing up in an ancient mythological context may not be used later on in non-mythologically-based contexts such as everyday tasks or in studied subject matter. In such instances, some numbers frequented by the mindset of a past culture may not be perpetuated by later variations of the same culture. (For example, some culture may have used the number "7" for defining some especial perspective, but later generations use the value much less or not at all.) But before providing an example, let me state a caveat: When someone says "Most" people or even "Everyone", or "All" people when describing any consideration, it needs to be fully recognized that none of us knows "Most, Everyone, All" people. We are not an omnipresent god-like figure in touch with everyone's mind and feelings.

It also is of need to point out that Cultural offshoots (such as the U.S. from Europe), may in some instances exhibit a larger usage of a particular enumeration, even though the perception may not make it into some social media preoccupation. Take for example in the case of a person's name. While the Romans did at times use three names for a person, some families retained the usage of two names; while it can be conjectured that all (or most) ancient peoples initially had only one name... be it due to some physical feature, some ability, or otherwise (paired) association(s).

In the late Roman society typically, citizens would be named using a three name system known as the tria nomina. This system distinguished Roman citizens from foreigners. The three types of name associated with this naming system are the praenomen, nomen and cognomen. These names would tell you a lot about the social status of a person. Not all Romans had three names; at the beginning of the Roman Republic only the patricians would use this three-name system, but as time went on more and more people in lower classes adopted the tria nomina system. (Three Names! How Ancient Romans named their children! by Lois Knight, April 26, 2020)

The point to be made is that the naming system followed a 1- 2- 3 sequential development; and in the cases where multiple words (more than three) are used to identify a person, one might suggest this is an expressed egotism beyond a common convention, such as in the case where everyone in a room is providing small numbers to be referenced as their favorite number while one person in the crowd is engaging in a type of one-up-manship by claiming a much larger number than anyone else, so as to stand out in the crowd by way of exaggeration.

Yet, let me provide a general list of (quantified) naming conventions from a few cultures:

• Chinese: Typically two names, last name first and first name last. (Chinese naming conventions)
• Vietnamese: Three names. [Family- Middle- Given] (Vietnamese name)
• Japanese: Two names: Surname- Given name (Japanese Name-ing Conventions)
• North and South Korean: Two names, Family name first... Given name second. (Korean name)
• Naming conventions in different countries
• In general, Arabic names are written in the same order as English: given name, middle name and family name.
• Most Spanish people (other than Argentines) have two surnames; the first inherited from the father and the second from the mother.
• The Middle Name Traditions in 8 Countries Across the World by Corey Whelan, May 24, 2021
• 7 Naming Customs From Around the World by Judie Haynes, 30 July 2015
• A guide to names and naming practices

The use of a single name is common practice due to familiarity or reputation. And aside from the names of individuals, we could also list the names of corporations, countries, street gangs, sports clubs, etc... The overall point being is that there is a limit as to how many words and/or symbols are being used to identify a person, place, and thing. This conservation of naming is another indication that humanity is being subjected to deteriorating environmental pressures forcing contractions as a survival mechanism. While some humans generally think it is better (smarter, easier, more efficient) to condense and symbolize (frequently referred to as "abbreviating" or "abbreviation"); it is commonly overlooked that the word "conservation" is equated with the idea of a "constant", in terms of being able to rely upon a given representation (like the conservation of energy idea) which helps to preserve an alliance with that which we call reality. Take for example the following reference:

In physics, a conservation law states that an isolated physical system’s particular measurable property does not change as the system evolves. These properties are sometimes called "constants of the motion."

In conservation laws, quantities are said to be "conserved," and the conservation laws that result can be considered the most fundamental principles of mechanics. In mechanics, examples of conserved quantities are energy, momentum, and angular momentum. The laws of conservation are exact for an isolated system. Here are some examples of Energy Conservation ideas in Physics: ((Laws of Conservation)

While it is easy to see the paired Mass -to- Energy (law of conservation) equivalence, the idea of equivalence as being a token representation for the presence of a conservation (and thus some similitude of constancy), may not come to mind in this explicit way. Instead, one may use the idea of "balance" or "cancelling out" as a substitute practice of conservation. We see a lot of this in Mathematics. Very often we see the use of the present two-patterned-dominant mathematics being used to describe conservations (constants) or at least used to support ideas which themselves sport an underlying tow-patterned focused frame of reasoning.

Because we humans frequently pair the ideas of conservation and constancy together while we ourselves are subjected to an environment undergoing incremental deteriorations and are required to make biological and psychological changes in accordance with as a survival mechanism; changes in conservation ideas (laws) will necessarily be re-worded or supported by various analogical forms and functions that are altered to comply with the incremental changes. Hence, the conservations change but we claim they aren't and defend alterations based on a variety of rationales such as having better measuring equipment, or more supportive data from multiple fields of application, etc... In other words, we do not view changes as actions of rationalization... or a coping mechanism to support alterations in our survival effort under deteriorating conditions.

If we look at an alternative (different) definition of Conservation, the word "symmetry" is used instead of the idea of pairing, dichotomy, duality, pattern-of-two, etc...:

Conservation laws are considered to be fundamental laws of nature, with broad application in physics, as well as in other fields such as chemistry, biology, geology, and engineering.

Most conservation laws are exact, or absolute, in the sense that they apply to all possible processes. Some conservation laws are partial, in that they hold for some processes but not for others.

One particularly important result concerning conservation laws is Noether theorem, which states that there is a one-to-one correspondence between each one of them and a differentiable symmetry of nature. For example, the conservation of energy follows from the time-invariance of physical systems, and the conservation of angular momentum arises from the fact that physical systems behave the same regardless of how they are oriented in space. (Conservation Law)

Conservation ideas reek of the old Yin/Yang balancing act of ideas. It is a common feature in present day Mathematics. If there were no other dominant pattern to make note of nor the presence of developmental themes following a 1- 2- 3 sequence, nor the attempt by many dualist's in seeking some harmony representing a third position, then the idea that the present model of Mathematics as an expressed practice of an antiquated theme would not have any need for us to make such an inquiry or take such a position of suggestivity. If there was noting significant in Nature using a pattern-of-three or other pattern, than a dominant reliance on patterns-of-two would have no need of examination.

In Biology, the balancing act is sometimes labeled as symmetry, even if one's individual interpretation allows for one side or the other to show dominance/passiveness in certain conditions. For example, one person may describe the mouth being dominant, while another person say that the anus is (under certain conditions). To a Musician the ability to hear may be most important, while a landscape artist prefer an ability to see. However, if one looks for symmetry in the array of human senses, one might say that the senses can be arranged hierarchically according to usage such as sight, hearing, smell, touch and then taste. However, different people may rank the senses differently and some may want to include other senses (third eye, third ear, ESP, subtle energy sense, etc...) as being more important. In addition, the loss of one sense may be met with a heightening of another sense as a compensatory reaction.

Getting back to the idea of symmetry related to pairing and related to dichotomization found in mathematics, let us note some different types of symmetry as they are identified in Biology, though different behavioral profiles exhibit their own hierarchy and frequently represent a syllogistic symmetry, where two items are contrasted to a third though pairing the two may at times be used to describe an idealized third option. However, if we were to look at all geometric forms, some are easy to describe in terms of symmetry, while the circle may cause some to be stumped. In order to classify a circle as a symmetrical object, one may resort to a type of dissection of overlay with one or more other ideas such as placing a north and south pole on it.

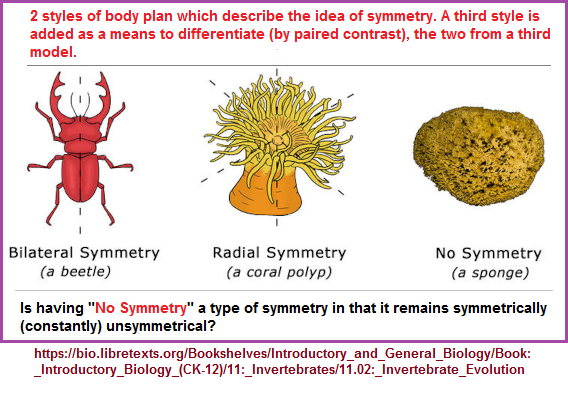
Sources for symmetry reference: Invertebrate Evolution, Symmetry in Biology

Least someone forgets to mention, let me state that Mathematics (like all subjects) is a system of naming practices, functions and ideas. While there are other ways of looking at items, conventions take place such as (for example) mentally framing a triangle as an object with three corners and/or sides, though one might cite it as the outline of a missing item which comes to the surface of an unnamed exterior placement. In other words, it is like an impression left over after an object is removed from a position in time and space which is not clearly identifiable.

Whereas we might say that "apparently" many people do/don't do-say-think-feel this or that or another, there is no actual quantification taking place. The usage of the word "apparently" can be used to reference a supposition without having to present an actual number that can be counted as an incorrect quantity. However, the same might be said for using the words much, more, many, a lot, numerous, etc... A person is referencing their own personal interpretation based on a personal tally sheet and not necessarily a catalogue of what one might assume to be hundreds, thousands, millions or "all" people. None of us know what most people actually think or feel, despite the number of times a person thinks or feels they have encountered a given reference. Just because we find a list referencing one or another pattern described as a commonality, it may be a commonality within the purview of a single person's experiences.

Take for example the idea that someone claims their martial arts, boxing or other sports club are "world" champions. If a person's "world" revolves appreciably around a given club or association, this may then represent what they interpret to be "The World" with respect to a given occupation or exercise.

Incidentally, just because someone asks several people in a crowd or even takes an online count of those taking part in a survey, doesn't mean that the result(s) reflect "everyone" or "all, or some, or many" people. There is no actual quantification of these word labels. The interpretation of what value such words actually relate to is arbitrary. Taking the word of a given writer's assessment without verification or quantifying a remark is little more than arbitrary guesswork, though they may indeed try to provide an honest appraisal and describe their limitations or the limitations of a given study. And even though I may list hundreds and thousands of "threes" examples, a similar amount (but not necessarily quality) might well be found using some other pattern (distinct number or some other type of pattern that could be enumerated).

Nonetheless, in my own assessment of enumerated patterns as a survey for patterns-of-three, I find an absence of the pattern and initially made a mental note of what pattern may or may not also be present. In so doing, enumerated patterns other-than-three come to the fore of consciousness whereby a mental grasp can be initiated as a visualization. Some number-relatable patterns show a greater frequency than others. One of these is a pattern-of-two when confronting Mathematics. When we place subjects with what appears to be a dominant usage of patterns-of-two into a separate list, some researchers may readily note that this same over-riding reliance on patterns-of-two show up in the ancient idea of Yin/Yang. This (knee-jerkedly) resembles a similarity of basic design suggesting there may be a close affinity to a similar type of antiquated mind-set, even if one argues for the position that they merely represent a fundamental feature of the overall design and this does not in itself state that such an organizational pattern and application reference an antiquated mindset. Even though I am inclined to believe that the top-heavy usage of patterns-of-two in Mathematics does indeed reflect an antiquated mindset placed into a modern context and adapted for a variety of tasks, this does not mean Mathematics (as a tool) is not an ancient method of thinking being preserved by an undisclosed sentimentality, like some religious custom handed down through generations.

One must wonder: "Out of all the infinity of numbers at our disposal, why is it that only a handful of numbers continue to crop up when we take into account all of human history from which to survey?" Such a conservation of number reliance begs the question of why this occurs... such as what is influencing humanity to repeat itself?

The following example of cultural usage of enumeration comes from: The Meaning of Numbers Among Different Cultures

The Number 3

Most people believe in the adage that "all good things come in threes." This is particularly true in Sweden, where people consider the 3 as a very lucky number. In Korea, they consider it as the luckiest number.

The association is different to what the people in Sweden believe. In Korea, the number three symbolizes control over ground and heaven because 1 represents the sky while 2 represents the earth. So adding the two numbers produces 3.

Italians associate the number 3 with balance and strength, represented by a triangle.

However, the Japanese and the Vietnamese avoid taking photos if there are only 3 people because of an old superstition that death will come to whoever is in the middle of the photo.

(Note, there is the old military-born notion that lighting three cigarettes with a single match is bad luck, based on the notion that by the time a third cigarette is lit, a sniper will have had enough time to focus their weapon in this direction.) Hence, all told, we have the occasion where the number three can be viewed in a dichotomous fashion as good or bad, depending on culture and context.

The common phrase for lighting three cigarettes with one match is "three on a match." One of its origin theories dates back to World War I. If three soldiers decided to smoke cigarettes together after dark and lit their cigs from the same match, superstition held that at least one of them would end up dead. Here's why. The strike of the match would alert an enemy sniper of the soldiers' presence. As the match burned to light the second cigarette, the sniper would have time to aim his rifle. Finally, as the third cigarette lit up, the sniper could shoot the third smoker. (Why is it bad luck to light three cigarettes with one match? by Debra Ronca)

In describing number patterns in different cultures, one needs to recognize that a person may be referring to a personal interest, a "sacred" number(s> related to myth and/or religion, or a system of counting such as in using a base 5, 10, 20, 60 or otherwise. Hence, do we count a process of enumeration as a "favorite" number of a (whole) particular culture, or as an imposed commercial system of accounting taught in an education system? One might also reflect on their preference of a labeled favorite number to consider that the origin of such may be based on an unrecognized or forgotten religious or personal context, to be distinguished from the favorite number(s) of others in their social circle or larger cultural environment. What numbers are used due to culture and which (if any) are due to a personal interest or reflect a cognitive mindset of "all" (most/many) humans?

Very often we find researchers commenting on the cultural differences of number usage by reverting to an apparent regurgitated standard of supplying examples from past cultures, namely Chinese, Greek, and Roman cultures... as if these three provide ample resources for reflection, and there is little need to include smaller cultures such as Australian aboriginal, Native Americans, African tribal customs, etc... However, one can surmise the need for a researcher to use frequently documented references because such accounts by so-called experts provides a means to defend against any who might want to argue for the inclusion of some other preferred culture when asserting the presence of a different number pattern usage. Nonetheless, what we should keep in mind is that number preferences need to be historically dated just as they are lumped together spanning decades and centuries of usage... or the degenerated usage thereof. An example of a (American) Cultural Anthropologist studying their own culture can be seen in Alan Dundez's "The Number Three in the American Culture" as posted by Michael Eck. Another listing can be found here:

1. The Number Three in the American Culture pg. 1
2. The Number Three in the American Culture pg. 2
3. The Number Three in the American Culture pg. 3

Note: I could not find a specific reference to a "favorite number" used by Australian Aborigines. When speaking of number usage, one might find someone trying to emphasize a complex form of counting being used to offset the (Westernized) notion that Aboriginal peoples do not count beyond the quantity five, where the notion of "one-two-three, many" might be indicated:

The overruling myth associated with Aboriginal people counting seems to be that we can’t or don’t count beyond four or five. Basically it is one, two, three, many and that is it. (Explainer: how does the Aboriginal numeric system work? by Shannon Foster, 1 February 2017)

Since time immemorial people have attributed sacred meanings to numbers. The most significant numbers for the indigenous population of North America are three, four, and seven, and they play an important role in the lives of American Indians: in their mythology, rituals and ceremonies, chants, literature, architecture, visual arts, households, etc. American Indian numerical symbolism has much in common with that of other traditional societies, but in some aspects it is unique. Mythology not only helps understand the meaning of certain numbers, but also regulates their use in daily and ceremonial life. (Numbers in American Indian Mythology by Oksana Y. Danchevskaya, Moscow State Pedagogical University)

Have you ever wondered why many African cultures and traditions attribute a level of importance to certain numbers; the most common of them being the number 7 and the number 4? (Significant Numbers in Africa by Admin, March 18, 2022)

African numeration system are numerous and varied. The most common are numeration systems based on 2, 5, 10, and 20 or a combination. (African Numeration (Number) System)

Let us note a similar ending in the Basque language to the three numbers 7, 8, 9 involving the letters "z" and "1" (Basque numbers)

As another example of enculturated number usage, let us note a few that may or may not stand the test of lengthened time as has some numbers (such as 3 and 7 and 2 or 4). Impetus for the following list comes from (10 Interesting Numbers in American Culture (Plus or Minus a Few) by Ethan Trexm, Jun 1, 2011)

• The 9/tenths usage for gasoline pump prices and the 99 cent rule-of-thumb for other goods prices.
• 24-7-365 reference for 24 hours of a day, 7 days of the week, 365 days of the year. (When looked at a bit more closely, we see the absence of the three numbers 1, 8 and 9... not including zero.)
• The number "ten" is not included as a "teen" number, though this is where the word "teen" originates from. Incidentally, you do not see a customary reference that the "teens" (13, 14, 15, 16, 17, 18, 19) are seven in number.
• "100 proof" for liquor as a midway point of determining the drunkenness value of a beverage. (This reference was a standard amongst teenagers when I was growing up several decades ago.)
• The Magical Number Seven, Plus or Minus Two. This is a classic psychology paper by George A. Miller. Unfortunately, far too many people focus on the "seven" portion of the title and do not look upon the title as a word math problem. Hence, one would thus see that three number values are being expressed (5-7-9). Like many other instances in human language, one or more numbers (or word) can be used to conceal one or more other words/numbers.
• Typically, one might say that a square is equated with the number "4" because of the quantity of its corners, and "3" is equated with a triangle, there is a recurring absence of number associated with a circle. In other words, why is it that human cognition references a usage of corners (like putting a puzzle together), but makes no cognitive in-road to enumerate a circle based on its own merits or profile?

With the word "puzzle" comes to mind the image of mathematic's different branches as different pieces which no one has yet thought to piece together, or else if they have considered it, have not publicly represented the idea in any convincing way... hoping to capture what it is that such a picture or map unveils.

PUBLIC NOTICE: The gauntlet has been thrown and the Battle Lines drawn. On one side of the line we have: How Imaginary Numbers Were Invented; where the Statement "Nature Likes Complex Numbers" is asserted by the commentator. And on the other side of the road we have those of us who assert that Nature Loves the Number Three. I tried to leave the following comment, but it would never post:

Very interesting presentation. However. I have to take an exception to the idea that Nature likes complex numbers. It is more likely that Mathematicians like equations which suggest the existence of a complexity that they alone are privy to best illustrating with a symbology consistent with their artistically linked model of conceptualization. Mathematicians have BIG EGOS despite all the pretensed humility. Furthermore, when we have hundreds of examples of Nature using simple numbers, one must question the rationale behind the statement concerning complexity. Here is a site which displays hundreds of simple numbers being used by Nature: https://www.threesology.org/

So what do you think? Does Nature prefer complex numbers or simple numbers... or perhaps both? Neither?... because you think Nature is being misinterpreted by both perspectives?

As a further thought on the foregoing reference, Mathematicians drool over themselves in speaking about the discovery of "imaginary numbers", when the same idea occurs in multiple other subjects and contexts, (yet Mathematicians want you to think their mind's have created something uniquely special instead of being just another formula for modeling a commonplace brain activity which shows up in a variety of ways). For example:

1. Religion's Imaginary Number is called God. Some think that "God" explains everything to those who can read and understand his/her/it's signs and symbols.
2. The Golden Fleece and Holy Grail are Legendary Imaginary Numbers... (let us say imaginary symbols or symbols of imagination).
3. Winning the lottery, Horse Race, or Card game bet is the imaginary number(s) for some.
4. Physic's Imaginary Number is called the GUT and TOE (Grand Unified Theory, Theory of Everything).
5. Infinity is an imaginary number- (line) for some.
6. Music's imaginary number might be called a Pure Note, a Grand symphony, etc., expressed in signs and symbols on music sheets.
7. Sport's athletes have their own imaginary numbers called "what if's"... what if I beat a record... (to achieve something that has not been achieved before or thought humanly possible, and yet define's a person's dreams).
8. For some, their imaginary number is cast in the idea of creating Cold Fusion, or Teleportation, or Time Travel, or a perpetual motion machine, or quantum computer.
9. In the past we had those who cherished the imaginary numbers called the Philosopher's stone, the Elixir of Life, or a communion with a spirit, entity, or other suggested (good or evil) force to empower oneself with.
10. Imaginary and Magical numbers are concepts frequently intertwined because they are brought up as fraternal twins (though commonly used as conjoined twins) in the underlying basic cognitive activity humans are born equipped with.

Hence, the term "imaginary number" is itself part of the same imagination which created it to fit the mindset of those who use numbers and associated symbols in a given context with a given label... by which to observe, investigate, and illustrate the reality they think they perceive, and want to convince everyone else that their perspective is the most unique, most informative, and the "best picture" of an overall scenery about some supposed reality they are trying to portray and want all others to accept as the definitive truth... whereby society will build itself around their views and thus perpetuate the reality they want to illustrate with made up symbols and expressions called equations. The public is often times much too gullible for its own good, such as for example, believing the recent balloons shot down were possibly Chinese, when it is the U.S. Military you need to be wary of. They like to make up stories and concoct fabricated information just as they did with the so-called weapons of mass destruction in the gulf wars... if not the US government nonsense about the events of 9/11.

Date of Origination: Tuesday, June, 21st, 2022... 4:31 AM
Date of Initial posting: Monday, August 8th, 2022
Updated posting: Friday, February 24th, 2023... 2:03 PM