8
(Static -vrs- Dynamic)
~ The Study of Threes ~
http://threesology.org
Visitors as of 2/27/2021

If we view an equation as a playing field and numbers or symbols as players ... with "functionals" or operationals (+, -, /, x, etc.,) as goal posts, boundaries, rules, bases, time periods, referees, coaches, scrimmage lines, etc..., all of the games display definable similarities; though players with unusual (radical or transcendental) and unknown (unexpected) abilities (singular or multiple) may create inequitable events to take place, resulting in a different outcome. Such is the case even if certain players are favored to provide a given outcome that one may overtly or covertly support {make a bet on). In other words, mathematics provides a certain type of uniformity to be relied upon, so long as the playing field of applied mathematics remains... at least, constant or regular, or with some measure of identifiable "normal"... enabling a constancy of equations and formulas for a large measure of certainty.
Here is one perspective on the idea of Uniformity in Mathematics:
Uniformity Conjecture
The uniformity conjecture postulates a relationship between the syntactic length of expressions built up from the natural numbers using field operations, exponentials, and logarithms, and the smallest of nonzero complex numbers defined by such expressions. The Uniformity conjecture claims that if the expressions are written in an expanded form in which all the arguments of the exponential function have absolute value bounded by 1, then a small multiple of the syntactic length gives a bound for the number of decimal places needed to distinguish the defined number from zero (Richardson 2002). Richardson (2002) has systematically searched for counterexamples, but not found any. (Uniformity Conjecture)
While uniformity of equations may be an asset in a supposed "level" (standard of equality) playing field, we assume the existence of constants which asserts itself as a problem:
(The) Constant Problem
Given an expression involving known constants, integration in finite terms, computation of limits, etc., determine if the expression is equal to zero. The constant problem, sometimes also called the identity problem (Richardson 1968) is a very difficult unsolved problem in transcendental number theory. However, it is known that the problem is undecidable if the expression involves oscillatory functions such as sine. However, the Ferguson-Forcade algorithm is a practical algorithm for determining if there exist integers ai for given real numbers xi such that:
a1 x1+ a2 x2 + ... + an xn = 0,
or else establishing bounds within which no relation can exist (Bailey 1988). (Constant Problem)
Note: the foregoing comment "equal to zero" is itself problematic in that the idea of whether or not zero is to be included— subjects equations to standards of assumed finiteness or infinity. Hence, we come face-to-face with a different wording for the idea of duality or a pattern-of-two. Similarly, in physics... when the notion of a parallel universe is conjectured (or the "dimer" in chemistry as well as the binary star grouping in Astronomy, though there are three types of star clusters: globular, open, and associations), we are confronted by the usage of a different vocabulary to describe a pattern-of-two referenced as a type of mirror-image, that we also encounter in the words/ideas of mirror-neuron, bipolarism, split-personality, divergence, fork, etc... The "twoness" of human thinking processes found in mathematics, needs to be compared with the lack of twoness and the presence of some other pattern... even though like the usage of a binary coding in computing as the present dominant standard, we see the same character profile in mathematics reasoning. This is a troubling issue not only because it appears most mathematicians are not recognizing the presence of "twoness", but upon being shown that such does in fact exist, they might well be dismissive or defensive, such as supporting the requirement by citing the numerous examples to be found in other subjects, but not then also taking into consideration the absence of such and noting the presence of some other recurring pattern; all of which describe an environmental pressure gradient forcing biology to defer itself to deteriorating environmental conditions by way of adopting rationalizations such as religion and the current state of nonsense politics with an increasing irrationality. Indeed. let us refer to the History of humanity as an Age of Irrationality amongst the currency of life forms now in vogue.
Even when we speak of possible (irrational, spiritual, hidden, transcendental, inter-dimensional), etc., identities existing outside, within, beneath, between, next to, etc... the configured constraints (constants, uniformities) of number usage (or symbolic substitutions); we speak of them from the perspective of known parameters. It is difficult to conceive of, much less illustrate an entity or identity that is beyond the conventions of that which is known or thought to be known. For example, I previously stated that I had to admit my inability for writing an equation to describe a form of mathematics which has never before existed. (Predictive Mathematical Models) The same is true for a musical note, chemical formula, physics theory, etc... Such cases are very much like inventing the wheel, draft animal yoke or boat rudder. The question of whether one actually invents something or merely discovers it by way of a change in one's perception or analysis thereof, are arguable points of reflection that can be asserted one way or another, much like the question of the chicken or egg origination. (Humorously, it is rather obvious that the chicken produced the egg so that the chicken could be born to produce the egg which preceded the chicken that was delivered by a stork which came from Lilliput and Blefuscu, even though one might prefer to consider the topic an item arising from a perspective seen Through the Looking-Glass . Interestingly, the latter mirror-image (dualistic logic) idea was produced by a mathematician by the name of Charles Lutwidge Dodgson who frequently wrote under the pen name of Lewis Carroll. Mathematicians very often remind me of ancient Chinese sooth-sayers prognosticating with the duality of yin and yang as a believed-in tried-and-true methodology from which personalized equations arise. The same is true who aspire to be knowledgeable by way of using the I-Ching's eight (so-called) trigrams which are actually bigrams.
Here is the reference previously used in the Predictive Mathematical Models page to describe the difference between a Trigram and Bigram:

Despite the idea of Uniformity in mathematics, the upcoming poem illustrates an ongoing blindness amongst mathematicians who preferentially see the world (or an equation) within the environmental perspective they are most familiar with. Uniformity of "play" (using fixed equations methods of known problems), delineates the usage of a given playing field with the same rules. Does mathematics exists in all kinds of playing fields, or a set few that have gained a popularity, like some sports being more popular than others? Does mathematics have a preference for the type of "ball" (particularized focus) it uses? (Some examples of balls are: golf ball, basketball, soccer ball, tennis ball, racket ball, billiard ball, football, softball- hardball- mushball, beach ball, volley ball, bowling ball, marbles, dice (square balls), tires as balls, badminton shuttlecock, tetherball, four-square ball, table-tennis ball, hockey puck, polo balls, etc...) In Ancient Rome (from who we get multiple "threes" ideas... possibly derived from Greek sources), there appears to have been three balls:
Among the Romans, ball games were looked upon as an adjunct to the bath, and were graduated to the age and health of the bathers, and usually a place (sphaeristerium) was set apart for them in the baths (thermae). There appear to have been three types or sizes of ball, the pila, or small ball, used in catching games, the paganica, a heavy ball stuffed with feathers, and the follis, a leather ball filled with air, the largest of the three. This was struck from player to player, who wore a kind of gauntlet on the arm. There was a game known as trigon, played by three players standing in the form of a triangle, and played with the follis, and also one known as harpastum, which seems to imply a "scrimmage" among several players for the ball. These games are known to us through the Romans, though the names are Greek. (Ball)
"Three" identities make up a basic equation, even if one, two or all three are unknown. Interestingly, three make up the foundation of double-entry accounting as seen in the following example:
What Is the Accounting Equation? Also known as the balance sheet equation, the accounting equation formula consists of three elements: Assets = Liabilities + Equity.
This equation should be supported by the information on a company’s balance sheet. The Accounting Equation is the foundation of double-entry accounting because it displays that all assets are financed by borrowing money or paying with the money of the business’s shareholders.
Attempting to describe an unknown equation, such as a new model of Calculus, requires a different playing field as many a "pure" mathematician would attest to in their attempts to discover new mathematical territories... though they routinely remain in the realm of using a three-element strategy. Along with the idea of a two opposing teams description seen in multiple types of games or gaming situations, we similarly pay witness to the presence of left and right sides of an equation because it is claimed that equality is symmetrical... otherwise noted as dichotomous... or two-patterned. We do not typically think in a one, three, four or larger-pattern frame of mind when constructing a basic idea of equality. Whereas in a social condition we may think of multiplicity in terms of equality or the nefariously used "equal opportunity" as an honest signification of proportionality, the idea of equality is typically seen in the image of a balancing scale. Such scales are not usually created to illustrate less or more than two identifies. Yet claiming equality as being symmetrical is like saying all life forms are bilateral in body form. Because all life forms (biologically based equation outcomes) are not all symmetrical, it pays us to look at the possibility of existing life forms (equations) which exhibit Radial and Asymmetrical forms. The usage of reverse engineering a math problem does not guarantee we will be enabled to pay witness to a basic design attributable to a basic cognitive structure.
While it is claimed that higher or more complex organisms tend to be symmetrical, on a very basic level, we can find symmetry in the presence of an IN mouth) and an OUT (anus), which is an arrangement that can vary with respect to placement, but nonetheless is a significant attribution for comparative anatomy, though debates can be seen regarding what is actually meant by mouth and anus. These two are frequently described in relation to one or more of the three Germ layers. Mathematically speaking, what we see is a recurrence of a two and three-pattern reference. Specifically, what appears to be taking place is a recreation of events occur in biology cropping up in mathematical operations in what can historically be mapped out as an evolutionary expression with starts, stops, stable forms, unstable forms, mutations, digressions, terrain specific species, predatory mathematics, social divisions: "worker mathematics"- "managerial mathematics"-, "owner mathematics", etc...
Embryologists and more especially those zoologists who are engaged in teaching must long have felt that there is some confusion, or at least want of precision, in the use of the word mouth. Sometimes it is used to mean simply the anterior opening of the alimentary canal; at other times a more special morphological significance is attached to it, and the term is used to denote the anterior opening leading from the ectodermal stomodaeum into the endodermal cavity or enteron... ... What has been said about the mouth applies with equal force to the posterior opening of the alimentary canal, or anus. In the early embryo the anus may be situated at the point where ectoderm passes into endoderm; while, usually in later stages if not from the first, it may be the opening to the exterior of a proctodaeal ectodermal invagination. ( Mouth and Anus by Edwin S. Goodrich, F.R.S. [Fellow of the Royal Society])
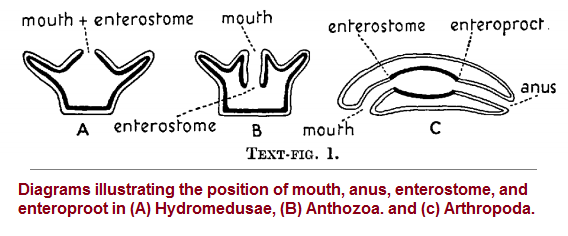
You may also find this link of interest: The Devil's Advocate and 3's Research, page 28
Another example of a basic biologically-based symmetry can be seen in the pairing of amino acids.
Abstract
A set of amino acid pairings are presented which may allow protein-to-protein information transfers. Amino acid pairing is only possible on a parallel ß ribbon and involves both the polypeptide backbones and the side chains. Model building revealed that of the 210 possible amino acid pairs of the standard 20 amino acids, no more than 26 could be built to meet standard criteria for bonding. Of these 26, 14 were found to be genetically encoded when the codons are read as if they paired in a parallel manner (i.e. in a manner reflecting the structural parallelism of the amino acid pairings); the other 12 pairings were derivatives of the coded pairings in which a single base of the codon triplet had been varied in accordance with Crick's (1966) "wobble hypothesis." Evidence for the pairings is presented from colligative studies of polyamino acids. Ways of testing the hypothesis further are suggested. Its implications for the Central Dogma and theories of the origin of life are discussed. (Amino Acid Pairing by bert Root-Bernstein; Michigan State University)
A "mirror-image" body plan relates to the visual spectrum involving light which is associated with the electro-magnetic spectrum of waves. If we view mathematics as a symbiotic life form, this then admits to a type of symmetry... where deeper and more complex relationships can be developed to the point of inter-dependency... which is the current state of the mathematics/human bond. However, it is not known what type of bond is taking place (ionic, covalent, and metallic.), or whether some other label should be used such as attachment, integration, blending, attraction, etc...
American poet John Godfrey Saxe (1816-1887) based this poem, "The Blind Men and the Elephant", on a fable that was told in India many years ago. It is a good warning about how our sensory perceptions can lead to misinterpretations... And how people can see the same thing in a completely different way... even though mathematics attempts to claim a uniformity by way of repetition and mimicry.
In the following poem, one can replace the word "men" with mathematicians, physicists, politicians, biologists, sociologists, anthropologists, archaeologists, etc...
| It was six men of Indostan To learning much inclined, Who went to see the Elephant (Though all of them were blind), That each by observation Might satisfy his mind... |
 |
 The First approached the Elephant,
The First approached the Elephant,And happening to fall Against his broad and sturdy side, At once began to bawl: “God bless me! but the Elephant Is very like a wall!” |
 The Second, feeling of the tusk, The Second, feeling of the tusk,Cried, “Ho! what have we here So very round and smooth and sharp? To me ’tis mighty clear This wonder of an Elephant Is very like a spear!” |
 The Third approached the animal, The Third approached the animal,And happening to take The squirming trunk within his hands, Thus boldly up and spake: “I see,” quoth he, “the Elephant Is very like a snake!” |
 The Fourth reached out an eager hand, The Fourth reached out an eager hand,And felt about the knee. “What most this wondrous beast is like Is mighty plain,” quoth he; “ ‘Tis clear enough the Elephant Is very like a tree!” |
 The Fifth, who chanced to touch the ear, The Fifth, who chanced to touch the ear,Said: “E’en the blindest man Can tell what this resembles most; Deny the fact who can This marvel of an Elephant Is very like a fan!” |
 The Sixth no sooner had begun The Sixth no sooner had begunAbout the beast to grope, Than, seizing on the swinging tail That fell within his scope (preferred discipline), “I see,” quoth he, “the Elephant Is very like a rope!” |
 And so these men of Indostan And so these men of IndostanDisputed loud and long, Each in his own opinion Exceeding stiff and strong, Though each was partly in the right, And all were in the wrong! |
 Moral:
Moral:So oft in The disputants, I ween, Rail on in utter ignorance Of what each other mean, And prate about an Elephant Not one of them has seen! |
A problem with using such a poem as the foregoing to represent an idea incorporating a non-religious context and subject, one must include a sort of legend in an effort to clarify its usage. For example, the Elephant can be viewed as (a given) reality being looked at by various mathematicians, physicists, Sociologists, Anthropologists, Historians, etc... from their respective vantage points from within their chosen discipline, as well as those who would think to indulge in a multi-discipline approach— thinking it advantages them and does not hinder them in a like-minded hunter's blind manner. The equations and comments given by the different mathematicians are a tell-tale indication of which means of groping they are invested in using. For example, one blind person may use a cane, while another has a given area laid out with particular items that they can memorize as a means of assisting in their navigation without the need for someone or anything else like a string of rope tied off along a corridor. Yet another may prefer to survey their perceived reality by way of reading the Braille described representation of one or more writers. In any regards, the equations and commentary being supplied illustrate the extent to which their particular blindness (or blinders on), have adapted by way of a compensatory effort involving one or more senses such as smell, sound, "sightedness" (partial blindness?), touch and taste. While one may prefer to see a given equation as a means by which greater clarity can be achieved, it also describes the kind of blindness and what method(s) of compensation are being used to help someone traverse the divide between one and another reality as one may attempt to describe.
Speaking of blindness and using it as yet another means to digress into a related metaphor, we can visualize the many different academic disciplines as types of hunters using their own kinds of blinds and tools, though hunters are more honest when describing the tools of their trade as fishing tackle, hunting gear, camouflage attire, field rations, etc., all of which are just as pricey as the research tools and accouterments of Academia. As they say, the only difference between men and boys is the price of their toys... whereas, it is impolite to dis-include the female species since so very many of them partake in their own forms of hunting; thus: The only difference between women and girls is the cost of their curls.
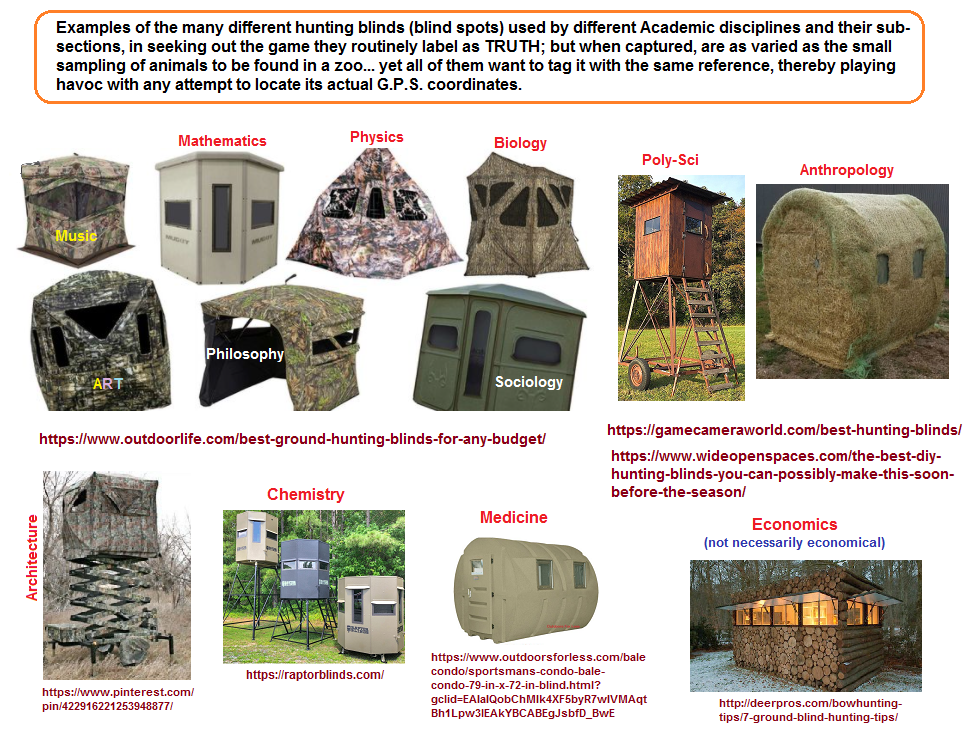
Here is a handful of different tools used by hunters (please note the usage of mathematical denominations when particular items are being selected for use). In short, hunters use a lot of numbers, philosophy, art, Drama, engineering, biology, physics, chemistry, etc., in their endeavors.
Various Academic research tools idealized for different discipline approaches; (This is intended to be analogically and metaphorically humorous. It is not too difficult to witness a professor acting like a gun-totting protector of some academic faith who slings the truth of their gun in the direction of a student trying to shoot them out of their perch and claim the class prize of having bested a professor in their knowledge. Students are always on the hunt for getting a better grade, better class position of notoriety, while others resort to their own types of becoming sacrificial bait, decoys, spotters, etc...
- Fishing pole; fly fishing, bank fishing, boat fishing, wading-fishing, etc... (And how many fishing expeditions have you been on in your search for a particular solution to a given problem?)
- Hunting knife: machete, Bowie knife, skinning knife, gutting knife, two-sided, serrated, all-purpose, etc...
- EnCampment tools: shovel, pick, hammer, rope, string, first aid kit, etc... (It is not rare to see a professor or student "camp-out" in a position of thought, or where they stand and teach, or where they sit and listen, etc...)
- Bow and arrows: compound/recurve Bow and specialized arrow- shafts, feathers and tips; cross-bow, etc... (How many arrows... as questions, have you shot in class? How many does a given instructor do? Do the shoot from the hip, into the air, or use alternative methods?)
- In-camp toy: blow-darts with and without poison, cards, etc...
- Club: baseball bat, iron pan, tire iron, etc...
- Manufactured or on-the-fly (concocted) {wait-and-see} hunting blind (concealments)...
- Enraged wife or Jealous husband (to scare of possible competition for the same prize, however defined)... (Need I really propose an explanation for this example?)
- Bait and tackle (frequently versatile for multiple hunting expeditions or unforeseen opportunities...) (Learning can take place anywhere at any time)
- Gung-ho kids (students to create creative "fires", douse fires, cleanup an argument, run errands of alternative suggestions, etc...)
- Long or short barrel Pistol or Rifle of choice: muzzle-loader, 30-06, 30-30, .308. .338, .375 magnum, .450, .45-70, AK-47, AR-15, AR-16, Glock 10mm, 45-caliber Glock, 50 caliber machine gun with scope, 22 cal, 25 cal, 38 cal, 44 magnum, 45 cal, etc...
- Shot gun: single/double barrel; 12 gauge, mossberg 500 tactical, sawed-off... (I frequently use a triple-barrel shot-gun approach)
- Hunting accessories: decoys, scent, traps, bait, etc...
- And if the typical array of academic inquiry tools do not work, one can always resort to dynamite, grenades, rockets, or forest fire.
In other words, the current model of the Gravitational expression is like a professor exhibiting slides or pictures of a journey (as would be the case before the advent of easily accessible and affordable motion picture equipment that has now been made available to everyone... whomever now owns a cellular phone (or is exhibited as a function on many common cameras with a motion-picture-making capability). The Gravitational Expression... needless to say, is static (non-moving, like a slide or single-image picture). This is how "they" (many equations) are written. The "movement" takes place in the mind of the equation reader, like the activity which was once widely practiced by those listening to a pre-television era radio station which might involve many sound effects to influence a corresponding image. Movement is acquired by way of a trained-in-the-old-way-of-visualization, based on proscribed assumptions. It is no wonder we can have millions of people involved in performing mathematics equations but produce so rarely few transcendent break-troughs.
Speaking of break-throughs which are routinely thought to occur with young mathematicians, while other areas such as philosophy, acting, sports, chemistry, physics, etc., sometimes exhibit older... more mature... more practiced individuals reaching a new-found pinnacle of expression and/or activity; I awoke one late evening (March 4th) 3 minutes before midnight with the dream-like thought that we find multiple intelligent people who are not smart, and because they are not smart we can say they are dumb. It was one of those off-the-wall Eureka! moments one can only laugh at. Hence, by reflecting on this new-found realization: what we find is multiple intelligently-smart dummies canvassing the different terrains of mathematics. HA! At some moment later when the laughter has at least subsided to the point where some semblance of rationale —current standards of accepted— sanity wrestled my now awakened consciousness to the light and breath of what we presently call reality... it then occurred to me, (as I mentally referenced different historical figures who have been described as a genius), that the best way to describe them (since they are acceptedly thought different... though still human (in most cases) from the "intelligently-smart dummies" group); is to appreciate the fact that creative people often exhibit a naivete' or distracted ness, or "space-caseness", or seemingly irrationality, or inclination to serendipitous peripatetic stumblings, or absent-minded professorness, or some other disposition framed as a quirkiness, fastidiousness, super-sanity that is commonly accentuated with the endowed socially-accepted label of eccentricity.
With respect to Mathematics (though we could include all human activity), there are three above-average categories used to define different levels of ability alas well as three below these... yet we do not claim three above them nor have anyone in mind who would rate in even the lowest "above average genius" level, however we might come to define such a category. Like the word "proof", we think the word "Genius" is the ultimate representation that human activity can achieve, unless someone claims that "Giftedness" supersedes being a genius and we thus use the first three in the following series as a prefix before the word "Genius" such as a "talented genius, gifted genius, genius-genius... as a means of describing some inclination that a person is somehow a mythologically created demigod in that their ability comes directly from a unique relationship with a god.
- Below average maths ability
- Average maths ability
- Above average maths ability, but not actually viewed as being talented, gifted nor a genius.
Talented: generally measured by a level of success associated with social visibility, and/or personal economics (If they had made "a lot" of money.), and/or exhibit leadership skills.
- Average talented person
- Above average talented person
- Highly talented person (also called a prodigy)
Giftedness:
Genius:
Yet, what of those who may be thought of as being more than the "common" garden variety of genius? Surely something like the following categories might well apply as an example:
- Above average Genius
- Super Genius
- Ultra-super Genius
In an attempt to categorize the possible types of talent, giftedness, and genius, I am reminded of the 3 X 3 ensemble referred to as the Hierarchy of angels. The hierarchy is a simplified expression of an underlying effort of innumerating what can be described as an unrecognized (mathematical) cognitive profile.
The most influential Christian angelic hierarchy was that put forward by Pseudo-Dionysius the Areopagite in the 5th or 6th century in his book De Coelesti Hierarchia (On the Celestial Hierarchy). Dionysius described nine levels of spiritual beings which he grouped into three orders:
- Highest orders
- Middle orders
- Lowest orders
During the Middle Ages, various schemes were proposed, some drawing on and expanding on Pseudo-Dionysius, others suggesting completely different classifications. Pseudo-Dionysius (On the Celestial Hierarchy) and Thomas Aquinas (Summa Theologiae) drew on passages from the New Testament, specifically Ephesians 1:21 and Colossians 1:16, to develop a schema of three Hierarchies, Spheres or Triads of angels, with each Hierarchy containing three Orders or Choirs.
Numerology and other number-related exercises in religion and other subjects, reference a similar brain activity. Even though present day "serious" partitioners of math and other subjects do not practice the ancient arts prior to the inception of so-called modern studies, the ideas of the ancient arts crop up in the minds of many people. To off-handedly be dismissive of or interpret such ideas as being stupid or foolish, overlooks the repeating recurrence of such thought patterns. Instead of discounting any value to the presence of such recurrences, they need to be collated as one would do in collecting data for establishing a statistical formula. In other words, there is relevance in that which many might consider to be irrelevant. Why does the human brain, despite so-called modern educational curriculums, attach itself to such patterns in the presence of alternative interpretations? If Florence Nightingale (as a statistician) had been dismissive of recurring observations that others were taking for granted, she might not have improved the care of the sick by introducing the ideas of better hygiene and sanitation based on the evidence she compiled for reforms.
Florence Nightingale is most remembered as a pioneer of nursing and a reformer of hospital sanitation methods. For most of her ninety years, Nightingale pushed for reform of the British military health-care system and with that the profession of nursing started to gain the respect it deserved. Unknown to many, however, was her use of new techniques of statistical analysis, such as during the Crimean War when she plotted the incidence of preventable deaths in the military. She developed the "polar-area diagram" to dramatize the needless deaths caused by unsanitary conditions and the need for reform. With her analysis, Florence Nightingale revolutionized the idea that social phenomena could be objectively measured and subjected to mathematical analysis. She was an innovator in the collection, tabulation, interpretation, and graphical display of descriptive statistics.
Not only can social phenomena, but psychological phenomena can also be subjected to enumerations from which can be derived statistical measurements related to evolution altered by the ongoing incremental deteriorations of the environment.
All present day practices of "serious" academic pursuits had early psychological roots such as astronomy from astrology, chemistry from alchemy, anthropology from bone collectors (or hoarders or bone throwing shamans), surgeons from butchers?, police officers from guards, etc... Such early types of pattern recognition and collating of different items, ideas, etc., have not been removed from the human mind of activity just because they are not familiarly practiced in school. The difference is that the old thinking patterns do not become appreciably altered for patterns used in subject areas which have become further developed. For example, a person may insist that numerology has some significance while another person is familiar with numerology but prefers to focus on using numbers in current mathematical models instead of numerological or mystical ones. Nonetheless, they both exhibit a basic currency of number usage.

As such, it is of necessity (for the sake of maintaining a continuity of logical standarness) to describe such geniuses in terms of the three foregoing terms used in the off-the-cuff jocular description of most mathematicians (and others) as being intelligently-smart dummies. It did not take too long before the whirrings and whizzings of the wheels in my mind to configure the only reasonable and rather rational moniker of a genius being a "dummy who is smartly-intelligent". E-gads! I became over-whelmed in the consideration that I, which is me, myself and I, as an infrequently described trio assimilated by Freud in his described Id- Ego- Superego, or the social class partitions of lower- middle- upper classes, or the philosophically constructed Major premise- Minor Premise- Conclusion... as well as other tripartite orientations... that a lightning bolt, or overhead light bulb, or firefly buzzings in and out of my ears; instructively conferred upon me a slap on the back of the head by the now famously recognized ancient muse who is enabled to travel the world-over like Santa Claus (and whose third identity is the tooth fairy in my more youthful days).
Simply put, by rearranging the same three words to effect the realization of a different point of view within the similarly-used linguistic scaffolding describing most mathematicians as being intelligent but remain too dumb to create a genius level of expressibility... (at least that which is viewed as being genius whether in one's own time period or some future one where their presumed genius will be understood); the three-coach train of thought that I was riding in (and waving at Einstein who was too distracted to see me as being relative to his other-worldly thought processing), retains its own linguistically confined syllogistic-like logic of mental cartography. Therefore, to recap: most mathematicians are Intelligently-smart dummies who are secure in their personal talent and creativity which enables them to perform sometimes vastly-memorized and sometimes complexedly-memorized equations which they routinely practice as a mnemonic aid (bringing to mind that mathematicians are those who are talented at memorization techniques and disciplined enough to carry out regiment mental tasks but highly deficient in the willingness to change one's mind if necessary, as a keynote prerequisite of genius activity); but are otherwise unable to, or afraid to breech the security-blanket and pacifier threshold of this routinization (and begin a type of loosely transcribed invitation as: "throw-caution-to-the-wind", call-of-the-wild motto) from which a trek into uncharted territory of mathematical probability and possibility calls to them like an incessant inner voice from which they can not stray too far afield or come face to face with the ogre of an uncertainty that may make them question their role in their present journey since it gives the impression of an absence of personalization... away from the regimentation; whereas we are left with the only answer to the foregoing word equation (story problem) as that which describes geniuses as dummies who are smartly-intelligent. Now that's what I call a moving equation... an "Accordian Calculus"!
| Categories | 3-patterned attributes | ||
| Earth | 3rd planet from a source of solar energy | ||
| Triplet Biological code | DNA | RNA | A- B- Z forms of DNA; 3 main RNA forms: mRNA-tRNA-rRNA...(+ others) |
| Triplet Human anatomy | A remarkable frequency of 3-patterned structures: List of Threes in human anatomy by Dr. McNulty (and associates) | ||
| 3 general racial categories | Asian variants | Dark skinned variants | Light skinned variants |
| 3 blood types | A: A- A+ AB+ AB- | B: B- B+ | O |
| 3 blood vessels | Arteries | Capillaries | Veins |
| Triune brain configuration | Neo (new) Mammal brain | Old Mammal brain | Limbic/Reptilian brain |
| 3 Spinal cord neuron categories | sensory | motor | interneurons |
| 3 part ear configurations | 3 divisions: inner, middle, outer |
3 bones (incus, malleus, stapes) |
3 semic circular canals (cochlea); 3 eardrum membranes |
| 3 part language, grammar, punctuation: | Subject- Object- Verb (trimodal structure); 1st- 2nd- 3rd person; past- present- future tense; periods- question marks- exclamation points; etc... | ||
| 3 categories of political systems | Authoritarianism | Democracy | Monarchy |
| 3 social classes | Upper | Middle | Lower |
| 3 desert-born Monotheisms | Christianity | Islam | Judaism |
| 3 leading types of mathematical definition |
Logicist definitions | Intuitionist definitions | Formalist definitions |
| math variables 1st + 2nd = 3rd |
Assumptions (plus...+)→ | Beliefs (equals...=)→ | Axioms |
| 3-part math computation and proofing | Inference, Induction, Deduction | add, subtract, multiply, divide | various syllogistic/logic approaches |
| 3 Earth models | Flat Earth theory/belief | Spherical Earth theory/belief | Triaxial ellipsoid theory/belief |
| 3 Universe models | Flat Universe model | Spherical Universe model | Triangular (saddle-shaped) model |
| 3-part Universe configurations: | Open- Closed- The something/nothingness as a separate reality or as a transitory state; Positive curvature- Negative curvature- Neutral curvature; Unidirectional expansion course, circular path course, elliptical path course; illusory expansion- illusory compression- illusory steady-state... |
||
With respect to the Wikipedia: Language of Mathematics the description says one thing but the reality is quite another, because it is often quite ambiguous, with words and concepts even mathematicians... to say nothing of students, come to decry as being the instigator of Cognitive Dissonance, not only mathematics but other genres of study as well... making the adventure of learning very often a labyrinthine structure strewn with language barriers for which a traveler must either learn navigate and slay the Minotaur, or ring the infamous bell of those calling it quits during special forces training where minds and bodies are sometimes asked to complete assignment that the instructor feels a candidate needs to know but will not actually make then more proficient nor an exemplary model of a given discipline, as attested to the desire by many mathematicians seeking to blaze a new trail into the territory of a more profound truth with its respective signs, symbols and overall language.
Cognitive dissonance refers to a situation involving conflicting attitudes, beliefs or behaviors. This produces a feeling of mental discomfort leading to an alteration in one of the attitudes, beliefs or behaviors to reduce the discomfort and restore balance.
While on the subject of psychology, a short digression into the psychology of Mathematics... or more to the point— Mathematicians, is to describe
Mathematics as a Narcissistic endeavour. However, the same can be said for all human activities, despite the language which might be used to contradict such a
perspective because those engaged in such activities consider their efforts humble, generous, sensitive, and multiple other virtues meant to dispel any
consideration other than any proportion of egocentricity. If one looks at the proposed qualities of a Narcissistic personality, we can quickly acknowledge that
such characteristics do indeed show themselves in different degrees not only amongst Mathematicians, but all people. No less, we can make out different levels
of different personality characteristics as well, though when someone creates a history of a subject such as for example, a history of mathematics, they may
well mention some good or bad behavior of a particular historical figure, but do not delve deeply into providing a psychiatric label or term to such behavior.
The same goes with the behavior exhibited by a given subject. That is, if we allow ourselves to think of a subject as a person, or an animal, or an insect, or
some botanical life form. One might even attempt to conjecture what type of cloud or weather pattern best expresses a given subject. Or what mood, what element,
which religion, or mechanical device, or kitchen recipe, or clothing style era, etc... While numerous comparisons can be made, I was unable to find any except
for one describing maths as an animal: If maths was an animal.
The language of mathematics is the system used by mathematicians to communicate mathematical ideas among themselves, and is distinct from natural languages in that it aims to communicate abstract, logical ideas with precision and unambiguity.
And while I am claiming that the Gravitation equation is motionless, Zeno of Elea is claimed by others to have said that motion was impossible; for which a few paradoxes were used to describe this exact belief. Let us take for example the paradox about a race between Achilles and a Tortoise:
 Smart By Design: Achilles And The Tortoise |
 IB Maths Resources: Achilles and the Tortise |
Date of Origination: 26 February 2021... 6:59 AM
Initial Posting:
June 9th, 2021... 10:45 AM