A Study of the Threes Phenomena
Visitors as of March 18th, 2025
Let's take a look at a short and very much abbreviated time-line of development, with the specific intent of itemizing a recurrence of patterns-of-three:
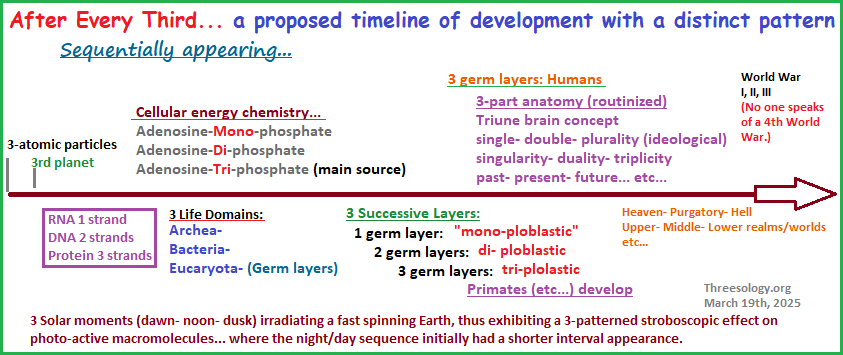
I am speaking about what appears to be fundamental patterns involving the disposition of Nature out of which biological Life emerges. However, not all expressed life forms are fundamental patterns. They may have some in their underlying developmental makeup, but they are more like a specialized cardboard box or other container, just as all of life is described as a vehicle to transport the triplet code of DNA around to improve its survivability. For example, the variety of birds, like the variety of humans (in personality, physical features, etc.,), may be more on the order of being equivalent to a single, double, triple base hit than a Home run, or... if not, they instead may each be a foul ball which grabs everyone's attention for awhile. If we were to dress all known types of hominid in baseball uniforms; are any of them to be viewed as Home Run Champions, or as dressed-up water boys that failed to make the grade to become a wished-for place on a winning team? Is today's humanity a winning team, or a Flintstone-like era of comedic dead-ends because it refuses to step beyond its self-defeating rationalization-based dualistic philosophies?
It is not difficult to understand what I am describing when I say "after every third." The patterns-of-three in physics preceded the pattern-of-three in the Earth's position which preceded the development of life with a triplet code. Even the chemistry of the developing Earth's atmosphere and oceans may involve various patterns-of-three such as a mixture of carbon 1-oxide (monoxide), carbon 2-oxide (dioxide), and molecular nitrogen... where it was a mixture being subjected to a 3-patterned strobe light (involving dawn-noon-dusk) which acted as a laboratory centrifuge under the conditions of a fast spinning Earth. Indeed, by looking for a given pattern, we can identify multiple patterns-of-three "coming on the heels" of another pattern -of- three (in relative terms of geophysical expanses of time). In some cases we can see an expressed 1-2-3 developmental pattern of a given pattern-of-three, and others may well be lost to time as to the enumerated values of their development, such as the idea we have not extant model of a life form with a single Germ layer (from the perspective of some researchers). No doubt that by focusing on the occurrence of a single pattern, be it Three or otherwise, we can come to identify sequences of events which may exhibit a sequence like that seen in the Fibonacci series, though the pattern is hidden from view because (using a methapor): "human perception gets too distracted when looking at the heavens and sees not but a multitude of stars but no recurring constellations".
Once pointed out, the Fibonacci series is easy to see. But if your mind is too distracted, despite your intelligence and rationalized approaches to a given genre of research in which you may be a leading figure in your field, that child-like curiosity and naïveté' you once used to begin you journey into your field of study are lost to perceptions which like-minded colleagues may have joined with you to develop a convention of thinking that gets in the way of being able to step back and take a fresh look at old information.
While the idea of recurring threes in other subjects (such as the triads of ancient Egyptian religion, Fairy tales and European Mythology is an old idea, and many former deliberate attempts to catalogue the recurring pattern have taken place, it has not been tried before in the overall development of life leading to a supposition involving the idea of a potential third consciousness and the problematic nature of Psychology, Mathematics, Education and other subjects, which rely on a philosophical foundation and clinical practice involving various dualities which are expected to appear as the dominant halmark of normalcy in human perception and thinking.
However, someone such as myself comes along and begins a dedicated journey into the perceptual realm of threes which is viewed in many respects as a taboo subject and is confronted by many set-in-place signs of disparagement (superstition, numerology, obsessive/compulsion, etc...) and conventionalize distractions (studies of duality in religion, philosophy, psychology, politics, mathematics, computer language, accounting, etc...); you have someone in your midst whose ideas may cause you to think that they need to be forced into compliance to the extent they must take hemlock (like Socrates) because my ideas will corrupt the young to think alternatively and not become victim to the status quo thinking which systems of education are presently engaged in, despite a desire to instill freedom of thought and expression. Hence, at this juncture in my life where I and others have journeyed into the depths of the "threes realm" where previous explorers may have gone but have left a map (written record) of such travels; if you get in our way, may your heaven help you as more and more are beginning a migration into the realization that Trichotomization is a vast uncharted territory that has stood as a mere myth for too long.
By adding more information to the time-line, a recurring pattern can become obscured unless it is specifically made reference to:
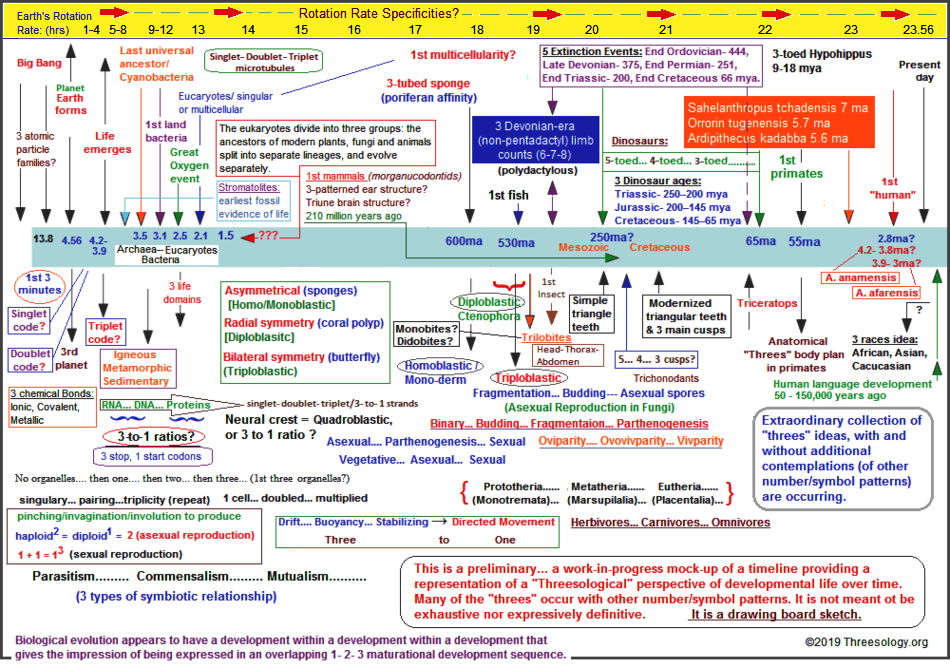
Let me provide a simple and very short list of 3-patterned occurrences with the intent of displaying that we can often find a set -of- three followed by another set of three in Nature...and that multiple other three-patterned ideas have followed suit... as if the "3" and variants are a recurring code. Granted you might want to intersperse examples of different patterns, but then you would run into the same problem of convincing others of the recurrence if you were to expect them to selectively pick out a given pattern as you do. It is frequently found that you have to simplify the intent of your message so that others can be accustomed to your representation.
- Triplet code in DNA (integrated as a 3-to-1 ratio)
- Recurring patterns-of-three design in particle physics (Protons- Neutrons- Electrons, 3 quarks/anti-quarks, etc...)
- 3 standard radiations of atomic particles: Alpha- Beta- Gamma
- Triple cocktail model of medical intervention (and prisoner execution)
- Boolean logic gate series used in computer code (simplified as: AND, OR, NOT...)
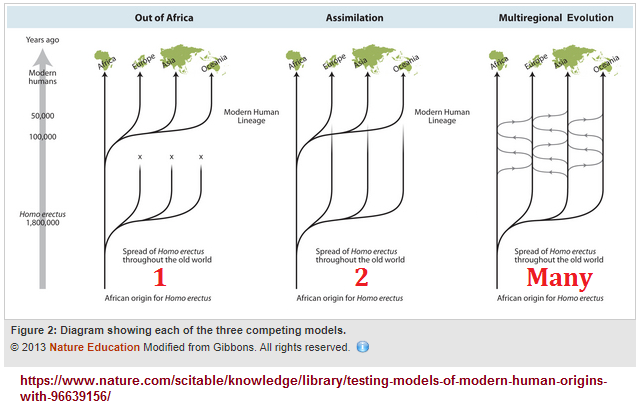
- 3 standard Human Origin Models: Out of Afica, Assimilation, Multi-Regional
- 3 trimester divisions of human pregnancy
- 3 colors (red- green- yellow) used for signal lights
- 3 fingers used to hold a pen, pencil, small paint brush
- 3 (Thumb- Index- Middle) fingers used by Middle Easterners to eat food
- 3 common eating utensils (knife- fork- spoon)
- Chinese adopted the use of 2 chopsticks
- Present day manufacturers have created multiple types of Knives- Forks- Spoons, but no actual "4th" item is named as part of the series, though some variant might be claimed as the 4th, 5th, 6th, etc...

- 3 traditional Biologically-based racial classifications: Caucasian- Asian- Negroid
- 3 Word-Order variants (Subject- Object- Verb)
- 3 common breakfast meats: Sausage- Ham- Bacon [USA]
- 3 common breakfast specialities: Pancakes- Waffles- French toast [USA]
- 3 item combo meals (Hamburger- French fries- Beverage) [USA]
- 3 common additions to hamburgers: onions- pickles- tomatoes [USA]
- 3 common condiment dressings used on hamburgers: ketchup- mustard- mayonnaise (others are speciality sauces) [USA]
- 3 common 8-hour shift divisions in manufacturing Morning- Afternoon- Night (sometimes there is an overlapping 4th shift)
- Emergency rooms at hospitals might exercise the use of two 12-hour shifts, while most businesses use only 1 shift.
- 3-foldness of Man is a common theme in some circles of philosophical tradition.
- 3 common vending machine coins: Nickles- Dimes- Quarters [USA]
- 3-phase standard electrical service (single phase also exists, creating a 3 -to- 1 ratio) [USA]
- 3 dominant fast-food cuisines: (American- Chinese- Mexican/Spanish) [USA]
- 3-day weekend holidays (typically the result of government-sanctioned practices) [USA]
- 3 orders of Society (Which Georges Dumezil elaborated on with a larger Indo-European assessment):
In the 11th and 12th centuries thinkers argued that human society consisted of three orders: those who fight, those who pray, and those who labour:
>
- The first order, those who fight, was the rank of the politically powerful, ambitious, and dangerous. Kings took pains to ensure that it did not resist their authority.
- The structure of the second order, the clergy, was in place by 1200 and remained intact until the religious reformations of the 16th century.
- (The 3rd order); The very general category of those who labour (specifically, those who were not knightly warriors or nobles) diversified rapidly after the 11th century into the lively and energetic worlds of peasants, skilled artisans, merchants, financiers, lay professionals, and entrepreneurs, which together drove the European economy to its greatest achievements.
Source: "Europe, history of." Encyclopædia Britannica, 2013.
- 3 copies was an old standard practice when using a type-writer.
- 3 colored business receipts remain in use by some businesses. [USA]
- 3 Traditional Library research options (Author- Title- Subject)
- Three laws of Motion (by Sir Isaac Newton)
- Three laws of Planetary Motion (by Johannes Kepler)
- Three part rule used in Fairy Tales, speeches, Nobel Prize offerings, Olympic winning/medals, etc...
- Three part common racing count: On/To your marks!- Get set!- Go!
- Three types of geological folds (undulation or waves in the stratified rocks of the Earth's crust.): Syncline- Anticline- Monocline
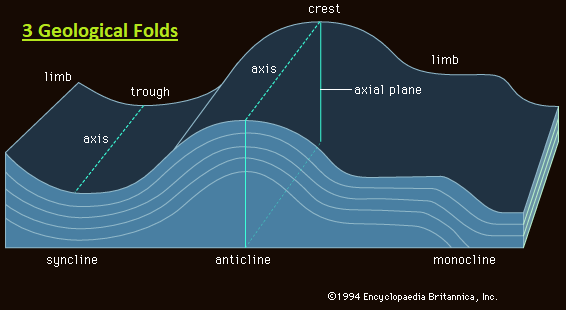
It should be noted that when one compiles "threes" and attempts to share the exercise with others, they may be met with the human inclination to compartmentalize information into separate subjects... which is sometimes used as a reason/excuse by some to refute any notion of connectedness. In other words, unless items in a list are compartmentalized under an existing label which a given person recognizes as being authoritatively signified like an esteemed University subject, they may find these others respondedly resorting to using some type of disparagement against those who do make one or another list. The more a given list is interpreted to be threatening to one's peace of mind established by a ritual of belief dependent on the presumed sanctity of a given subject's domain of established (and thus authenticated) inquiry, the more virulent in opposition they may become. Hence, a pattern-of-three in particle physics followed in history by the advent of a planet in the 3rd position of a solar system upon which life has come to grow, is a correlation too far removed from the accepted parameters of inclusiveness allowed by some investigators of natural phenomena— who may readily come to claim some (meant to be laughably absurd) outlandish example as a similar type of logic... all in an attempt to retain their desired area of study (as a pronounced absolute truth) in a very narrow enclave of consideration that they have a measure of control over.
The idea of a recurring pattern-of-three, much less a 3-to-1 ratio may never come to the mind of viewers unless such patterns are deliberately made reference to. If a recurring pattern takes place in a given subject that is one thing, but if you are an eclectic thinker looking at information from different subjects and claiming to see a similar pattern, you might be called a nut, fruitcake or someone indulging in a non-logical frame of thinking... even though every single subject had its initial beginning in the mind of someone who recognized some pattern that others had not done so, or if they had, not with an enhanced model of representation and explanation.
After every third we can recognize the End of a Beginning or the Beginning of an End.
I'm actually not trying to be cryptic (nor enigmatic) with the foregoing statement... even though it may sound like some Chinese Mystic's word salad. An explanation can be gleaned by using baseball as an analogy. For example...:
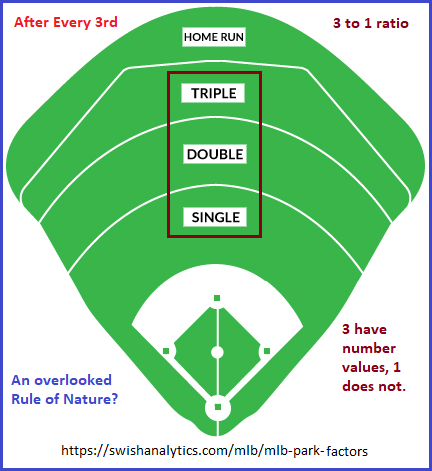
- After three bases, a scoring run is achieved, and in some instances may be referred to as a Home run. The Home Run is not a "4th base", but is a culminated (non-enumerated) achievement of the first 3 enumerated bases.
- Before the dedicated use of a three-strike rule (which can otherwise be labeled a code)... {before three strikes have occurred}, we have the start (beginning) of an inning. Let us call this the bottom of an inning (due to the style of score cards used). After three strikes, the other team gets an opportunity to bat with the three-strike rule applied as well. Let us call this the top of an inning. After both teams have struck out, a new inning begins. Typically there are 9 innings, (or one might view it as a 3 X 3 framework.) Hence, before 3 strikes, we find the beginning of an inning's end. After 3 strikes is the beginning of the end of that portion of the inning and signifies the ending of a new beginning for the next team.
- After "3 balls" are called by an umpire, the one following produces a mandatory walk for the batter to 1st base.
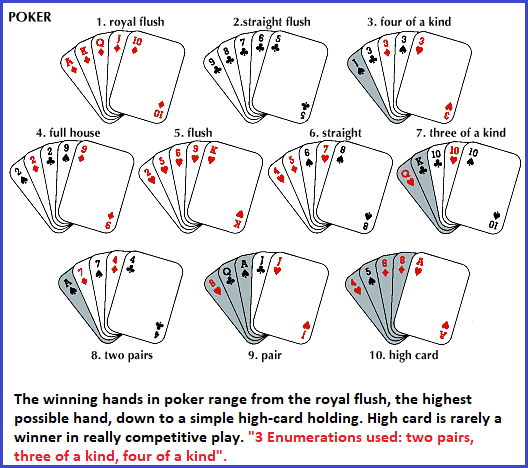
- Distinctions are made to indicate areas of a baseball field where single, double, triple and Home Run hits may be achieved. (Note that the first three
are typically aligned with enumerated values just like we see in playing the game of poker where a person can have:
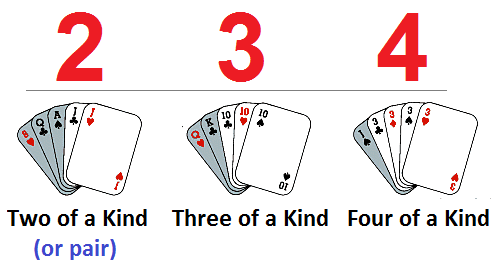
- 2 of a kind (also called a pair)
- 3 of a kind (do some players call this a trio?)
- 4 of a kind
The 3 -to- 1 ratio is an overlooked repeating value to be found not only in biology but multiple subjects. An illustration of Mendelian genetics may be helpful, while further on in the discussion I will introduce some others. Necessarily so, the reader should realize I didn't make up the examples, they are already existing, I simply put them together and arranged them with a unifying idea, much like others have done when presenting new theories. 3 -to- 1 ratios abound in different subjects, but have not been brought to the fore as a repeating pattern of human cognitive activity which can be paired to a distinctive environmental influence, namely the Sun and its three "moments/phases" (dawn- noon- dusk):
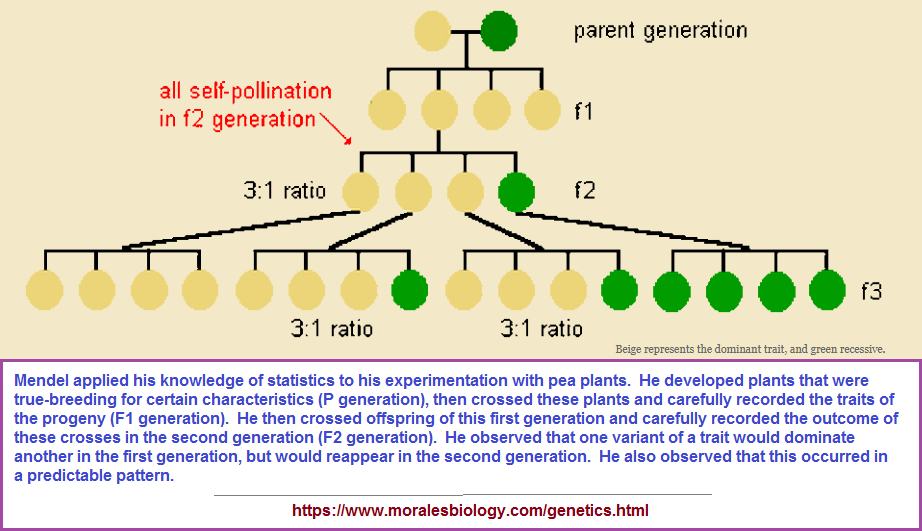
It is not customary to refer to the above pattern as a "4". However, a reference of "4" (such as four fundamental forces of Nature) is frequently used and the notion that what is being looked at can be viewed as a 3-to-1 ratio never comes to mind, simply because it is a pattern that is not widely recognized as existing and is therefore not being taught in school or written about.
The "2, 3, 4" enumerations are a collective set-of-three, while additional would-be enumerations are provided with word-names. Just like we don't typically hear someone referring to the Home Base/Plate as the 4th base. Such uses indicate we are dealing with a peculiarity of human cognitive activity that is not limited to these types of games and apparently was used in the development of counting systems in ancient times, though anything beyond the count of "2" was referred to in some sense of a linguistically relevant "Many" (or much, alot, bunch, heap, pile, etc...). We find the 3-to-1 pattern in multiple serious venues of study from Physics to Biology as well as everyday contemplations, though apparently most people are oblivious to such a recurrence since the knowledge of such began with me concentrationally describing its presence. Such a recurrence portrays not only human language and brain activity, but environmental circumstances whose origin may have begun billions of years ago, as indicated by the 3-to-1 ratio pattern found in genetics. Such a pattern can be seen in the description of the 1 Sun with 3 Phases (dawn-noon-dusk), which suspiciously looks like the origin of the Christian Trinity stemming from ancient solar-focused practices of worshipping Nature (sometimes incorrectly labeled as solar worship).
While the reader may want to claim that using the phrase "3-to-1" is merely a semantically twisted way of saying "4", they actually overlook an important distinction which needs to be made about human thinking. Similarly, we can find the pattern represented as a 3 and 1, or 3 into 1 as separate distinctions. It describes a proportion within a set, and not an enumerated sequence to be elaborated. For example, (1-2-3) is the same set, but so is (xxx-xxx-xxx). The so-called 4th place is the 1st position of a potential second part of a potential 2-part series (in this example), though the overall potential may involve multiple sets-of-three that may never actually be achieved due to incremental deteriorations taking place in the planetary sphere of changes. (Existing potentials both in the human sphere and sphere of Natural events does not guarantee an actual realization. In other words, though a person has potential, this does not automatically guarantee that potential will be realized to its fullest.) The "3 to 1" ratio takes place in multiple areas in which human mental activity is applied, but so too can we find instances of 3 to 2 (that some observers may count as five) or 3 to 3 (counted as a six), 3 to 4 {or as a 3:3:1} (counted as a seven), etc...
Interestingly, Native American neighbors on one Sunday decided to play a recording of drum beating to which they referred to as a pattern-of-four, but was actually three beats followed by a pause and then a single beat. Hence, I suspect that before the Native American adopted a serial counting method, there was an external influence which described their usage of 3 to 1 ratios as patterns of four, and they adopted this pattern of referencing as a dominant recurrence. One must wonder when, where and under what circumstances the count of "4" was used, since it is not of Native American origin. As in many cases, Anthropological descriptions are frequently filled with their own cultural bias. In most instances we see Anthropologists referencing themselves in terms of Nationality, religion, educational status, gender, etc., first, and afterwards as an Anthropologist. Indeed, if we were to look at another tribe that may reference themselves as using the value of "5" with greater regularity than any other pattern, we might well see a distinct 2 + 3 (or 3 + 2) pattern. The use of the "5" was influenced by some outside source. Indeed, if we look closely at our hands, in most cases we see fingers of different length, and only by calling them fingers do we collectively associate them as a group and call that group five. Like human usage which designates individual fingers for rings, gestures, vaginal stimulation, picking one's nose, cleaning one's eye corners, etc., each of them might actually need to be referenced in terms of singular distinctiveness (or less then 5) and not as a collectivity.
As an aside interjection, let me provide an excerpt from history which references a 3 to 1 ratio which occurred with Albert Einstein's thinking about an important topic:
(A 3 -to- 1 ratio) To derive his 1917 cosmological model, Einstein made three assumptions that lay outside the scope of his equations.
- The first was to suppose that the universe is homogeneous and isotropic in the large (i.e., the same everywhere on average at any instant in time), an assumption that the English astrophysicist Edward A. Milne later elevated to an entire philosophical outlook by naming it the cosmological principle. Given the success of the Copernican revolution, this outlook is a natural one. Newton himself had it implicitly in mind when he took the initial state of the universe to be everywhere the same before it developed "ye Sun and Fixt stars."
- The second assumption was to suppose that this homogeneous and isotropic universe had a closed spatial geometry. As described above, the total volume of a three-dimensional space with uniform positive curvature would be finite but possess no edges or boundaries (to be consistent with the first assumption).
- The third assumption made by Einstein was that the universe as a whole is static—i.e., its large-scale properties do not vary with time. This assumption, made before Hubble's observational discovery of the expansion of the universe, was also natural; it was the simplest approach, as Aristotle had discovered, if one wishes to avoid a discussion of a creation event. Indeed, the philosophical attraction of the notion that the universe on average is not only homogeneous and isotropic in space but also constant in time was so appealing that a school of English cosmologists—Hermann Bondi, Fred Hoyle, and Thomas Gold—would call it the perfect cosmological principle and carry its implications in the 1950s to the ultimate refinement in the so-called steady-state theory.
- To his great chagrin Einstein found in 1917 that with his three adopted assumptions, his equations of general relativity—as originally written down—had no meaningful solutions. To obtain a solution, Einstein realized that he had to add to his equations an extra term, which came to be called the cosmological constant. If one speaks in Newtonian terms, the cosmological constant could be interpreted as a repulsive force of unknown origin that could exactly balance the attraction of gravitation of all the matter in Einstein's closed universe and keep it from moving. The inclusion of such a term in a more general context, however, meant that the universe in the absence of any mass-energy (i.e., consisting of a vacuum) would not have a space-time structure that was flat (i.e., would not have satisfied the dictates of special relativity exactly). Einstein was prepared to make such a sacrifice only very reluctantly, and, when he later learned of Hubble's discovery of the expansion of the universe and realized that he could have predicted it had he only had more faith in the original form of his equations, he regretted the introduction of the cosmological constant as the “biggest blunder” of his life. Ironically, observations of distant supernovas have shown the existence of dark energy, a repulsive force that is the dominant component of the universe.
Source: "Cosmology". Encyclopædia Britannica, (2013).
In the realm of Mathematics, Set theory is a well defined discipline of simplistic thinking often misunderstood because of the symbolic language being used and the way it is described by practitioners of the craft. In their language, the "1-2-3" designations would be called elements or members of a set. Yet, the 3 members of a described set can be viewed as a cumulative single member (or element) of a larger set that might be termed a Universal set or parameter of occurrence.) For example, let us say the a Universal set contains three sets of members [(123)-(456)-(789)]. It's pretty simple stuff that anyone in the US is familiar with by simply looking at their Social security number which is displayed as 3 divisions of 3+2+4 numbers: (123)-(45)-(6789).
Note: The single source of Mathematics appears to be that of duality striving to develop a triplicity, just as the Yin/Yang elements were placed into three-part configurations and called a triad, though they actually remained as embellished dualities (Usage of 1 and 2 lines arranged into a pattern of three, while no actual 3-line configuration was ever applied). Similarly, while mathematics has developed three-part equations and a discipline called Trigonometry, it invariable retains an underlying usage of dualities.
In fact, this may be similar to the criteria under which Evolution did, does or will work. (A set of 3 occurrences followed by 2 and then followed by 4.) Or, due to the multiplicity of 3-to-1 ratios, Evolution may be using a (3) + (1) + (????)... Suggesting a currency of dynamic activity not yet fully grasped, or is malleable but still confined to some overall Universal set of possible activity because it is being imposed upon by an incrementally deteriorating planetary environment. Set theory, just like all of mathematics is pretty simple stuff, so long as you remember its underlying scaffolding is duality based, just like we find in the Yin/Yang idea (followed by the so-called I-Ching triads which are actually Byads), and the binary computer language, and of course, Binomial Nomenclature.

However, set theory is made more complicated than it needs to be because practitioners want to feel and make others think they are involved in some sophisticated intellectual enterprise that is not applicable to most commonalities of concern, but is particularly applicable to an intellectual realm of inquiry reserved for specialized thinkers (who sometimes want to make themselves appear to be smarter than they actually are)... much like the attitude we see in numerous other subjects that take on a specialized symbolism and vernacular as a weapon, shield, fortress or series of secret passwords needed to surmount in order to reach an inner sanctum to a sacred enclave of revelation and understanding... and any outsider who looks behind the (wizard of oz-like) curtain are said to be mad, heretics, infidels, or otherwise ostracized as an outsider or threat.
Set Theory:
(A) branch of mathematics that deals with the properties of well-defined collections of objects, which may or may not be of a mathematical nature, such as numbers or functions. The theory is less valuable in direct application to ordinary experience than as a basis for precise and adaptable terminology for the definition of complex and sophisticated mathematical concepts.
Between the years 1874 and 1897, the German mathematician and logician Georg Cantor created a theory of abstract sets of entities and made it into a mathematical discipline. This theory grew out of his investigations of some concrete problems regarding certain types of infinite sets of real numbers. A set, wrote Cantor, is a collection of definite, distinguishable objects of perception or thought conceived as a whole. The objects are called elements or members of the set.
The theory had the revolutionary aspect of treating infinite sets as mathematical objects that are on an equal footing with those that can be constructed in a finite number of steps. Since antiquity, a majority of mathematicians had carefully avoided the introduction into their arguments of the actual infinite (i.e., of sets containing an infinity of objects conceived as existing simultaneously, at least in thought). Since this attitude persisted until almost the end of the 19th century, Cantor's work was the subject of much criticism to the effect that it dealt with fictions— indeed, that it encroached on the domain of philosophers and violated the principles of religion. Once applications to analysis began to be found, however, attitudes began to change, and by the 1890s Cantor's ideas and results were gaining acceptance. By 1900, set theory was recognized as a distinct branch of mathematics.
At just that time, however, several contradictions in so-called naive set theory were discovered. In order to eliminate such problems, an axiomatic basis was developed for the theory of sets analogous to that developed for elementary geometry. The degree of success that has been achieved in this development, as well as the present stature of set theory, has been well expressed in the Nicolas Bourbaki Éléments de mathématique (begun 1939; "Elements of Mathematics"): "Nowadays it is known to be possible, logically speaking, to derive practically the whole of known mathematics from a single source, The Theory of Sets."
Source: "set theory." Encyclopædia Britannica, 2013.
H.O.B. note: Trichotomization will one day become recognized as a distinct branch of philosophical inquiry applicable to many subjects.
Note: "Axioms" are a set of rules that everyone agrees on, whether there is evidence for such a rule or not. For example, some people like to play sports, board or gambling games according to a set of written rules, while others may make up rules per the dealer's or collective players choice. Sometimes a single dominant player states (demands compliance to) what is and what is not acceptable. In other words, axioms are made-up rules (like laws) everyone is supposed to comply with in order to be viewed as some legitimate player... though those who don't sometimes find themselves creating a new branch of thinking about a given problem and find a solution that has stopped multiple generations of investigators (who followed the rules in order to be viewed as a valid participant in the respective game). However, rule breakers are sometimes found to be cheaters or those who want to take shortcuts and yet identified as a legitimate player of a particular game, when they actually are little more than being rude, crude, and lewd in their thinking and expect their behavior to be respected and recognized as original/creative, insightful and innovative thinking deserving of some grand prize, position and overall favorability.
Axiom: in logic, an indemonstrable first principle, rule, or maxim, that has found general acceptance or is thought worthy of common acceptance whether by virtue of a claim to intrinsic merit or on the basis of an appeal to self-evidence. An example would be: "Nothing can both be and not be at the same time and in the same respect."
In Euclid's Elements the first principles were listed in two categories, as postulates and as common notions. The former are principles of geometry and seem to have been thought of as required assumptions because their statement opened with "let there be demanded" (e-testho-). The common notions are evidently the same as what were termed "axioms" by Aristotle, who deemed axioms the first principles from which all demonstrative sciences must start; indeed Proclus, the last important Greek philosopher ("On the First Book of Euclid"), stated explicitly that the notion and axiom are synonymous. The principle distinguishing postulates from axioms, however, does not seem certain. Proclus debated various accounts of it, among them that postulates are peculiar to geometry whereas axioms are common either to all sciences that are concerned with quantity or to all sciences whatever.
In modern times, mathematicians have often used the words postulate and axiom as synonyms. Some recommend that the term axiom be reserved for the axioms of logic and postulate for those assumptions or first principles beyond the principles of logic by which a particular mathematical discipline is defined. Compare theorem.
Source: "axiom." Encyclopædia Britannica.
Another use of a "two category" first principle is found in the Binomial Nomenclature developed by Carolus Linnaeus:

Linnaeus's most lasting achievement was the creation of binomial nomenclature, the system of formally classifying and naming organisms according to their genus and species. In contrast to earlier names that were made up of diagnostic phrases, binomial names (or "trivial" names as Linnaeus himself called them) conferred no prejudicial information about the plant species named. Rather, they served as labels by which a species could be universally addressed. This naming system was also implicitly hierarchical, as each species is classified within a genus. The first use of binomial nomenclature by Linnaeus occurred within the context of a small project in which students were asked to identify the plants consumed by different kinds of cattle. In this project, binomial names served as a type of shorthand for field observations. Despite the advantages of this naming system, binomial names were used consistently in print by Linnaeus only after the publication of the Species Plantarum (1753).
In his own lifetime, Linnaeus became something of an institution in himself, as naturalists everywhere had to address him directly or at least his work in order to determine whether specimens in their collections were indeed new species. The rules of nomenclature that he put forward in his Philosophia Botanica rested on a recognition of the "law of priority," the rule stating that the first properly published name of a species or genus takes precedence over all other proposed names. These rules became firmly established in the field of natural history and also formed the backbone of international codes of nomenclature—such as the Strickland Code (1842)—created for the fields of botany and zoology in the mid-19th century. The first edition of the Species Plantarum (1753) and the 10th edition of the Systema Naturae (1758) are the agreed starting points for botanical and zoological nomenclature, respectively.
Source: "Linnaeus, Carolus." Encyclopædia Britannica, 2013.

Initial Posting: Tuesday, March 18th, 2025... 10:03 AM
Updated Posting: Sunday, March 30th, 2025... 12:59 AM