~ The Study of Threes ~
http://threesology.org
Visitors as of August 8th, 2022
| Page 1 | Page 2 | Page 3 | Page 4 | Page 5 |
| Page 6 | Page 7 | Page 8 | Page 9 | Page 10 |
| Page 11 | Page 12 | Page 13 | Page 14 | Page 15 |
| Page 16 | Page 17 | Page 18 | Page 19 | Page 20 |
In one version of the game, the player tosses a small, flat marker such as a stone or a beanbag into the first numbered space. If the marker does not land clearly in the correct space, without touching a line, the player loses a turn. If the stone does land fairly, the player hops on one foot to the second square and thence through the succeeding squares, in order and without touching a line, falling, or dropping the trailing foot. In some diagrams there are certain pairs of squares where the player jumps with both feet. In other diagrams, certain squares may designate rest spaces, in which the player may put both feet down. Upon reaching the last numbered square, the player turns and moves through the spaces as before, lifts the marker, and hops out of the diagram. A player who completes the diagram without making a mistake may continue, tossing the marker into the second square, hopping into the first space then over the second and into the third, and so on, until the whole diagram has been played in this manner. On completing the diagram, the player may initial any one of its spaces, which space the other players must then avoid, although the initialing player may use it as a rest space. The game ends by mutual consent or when all spaces have been initialed. The player who has initialed the most spaces is the winner.
In a common variation, the marker must be kicked with the hopping foot from space to space. Or the player tosses the marker into the first space, then hops on one foot into that space and kicks the marker back across the base line and out of the diagram, continuing this procedure for each space in sequence. In Hinkspiel, a German variation, a player who completes the sequence turns away from the diagram and tosses the marker over her shoulder. The space in which it lands is her "house," a rest space that the other players must then avoid unless its "owner" gives them permission to use it. Croatian children play skola ("school"), which refers to the squares as first through sixth grades of school. Among Igbo girls in Nigeria the game is known as swehi. The diagram is drawn in sand, and a stone or a ball of crushed leaves is used as a marker. The rules resemble those in the German game of Hinkspiel. In swehi, if the player's stone is tossed on a line, she is out of the game. At the end of the game, the players make drawings in each of the squares.
Hopscotch may also be played with a spiral diagram (this variant is known as escargot in France, for the spiral of the snail shell), in which players hop on one foot to a central rest spot and then back out again. Each player who succeeds may initial a space. The game continues until it becomes impossible to reach the centre or until all spaces are initialed. ("hopscotch." Encyclopædia Britannica, Ultimate Reference Suite, 2013. [No specific author is listed.])
In the development of enumeration related to quantity, the idea of pairing is often described in terms of a one-to-one correspondence, such as one spear represented by a reproduced image of a spear, arrow, or knife, which resembles a one, or a line. In any respect, different cultures arrived at the concept of enumeration related to quantity perhaps initially in the same frame of orientation as the counting behavior ascribed to different animals, in that their use of some supposed number-quantity resembles what humans identify as being a quantitative number. As such, this limits the ability of humans from being able to access the use of number or quantity in other life forms such as insects, which may use a different modeling thereof. In other words, if a life form uses enumeration consistent with what humans identify and label as number and quantity, then the life form is granted the privilege of being assigned the capacity of having some measure of a mathematical identity, however crude or primitive a human observer and cataloguer wants to bestow upon it. In any case, thus far humans have encountered life forms exhibiting rudimentary models of being able to count, if at all this is actually what is taking place, and if all this is actually what human behavior is involved with and not some other activity which is not yet understood nor even realized as taking place. In other words, that which we call mathematics may represent a rudimentary beginning of some other quality or capacity humans have not as yet realized as being the initial first steps or crawling stage of human consciousness. In one era human behavior will be interpreted and labeled one way and then in another era it is interpreted and labeled differently. Thus, every single subject present day humans are involved with may be little more than rudimentary... primitive exercises in that which is yet to be developed fully, or become similar to a vestigial organ after it is replaced by some other functionality or simply fall into disuse.
When we think of pairing in the context of a one-to-one correspondence designated as counting, it is not typical to view such a pattern-of-two architecture in different ways. For example, the Yin and Yang correspondence is a type of pairing like a left and right shoe. In some cases pairing may occur but placed into a three-patterned configuration such as a six-legged insect. In other instances we may have a doubling of an organ or an organ with a dual function such as a heart that has three layers, or a bicuspid (mitral) valve and a tricuspid valve, but no distinctly described (enumerated) monocuspid. Similarly, we have a single pair of lungs with the right side have three lobes and the left side having two lobes, which is a similar enumerated arrangement to the valves of the heart in the sense that the right side of the heart has the tricuspid and the left side has the bicuspid. Both organs are singular which engage in and in/out duality possessing structures corresponding to the same sides of the body that we can further describe in terms of body functionality when we take into consideration that when a person experiences a stroke in the left hemisphere the right side of the body is affected, and when a stroke is experienced in the right hemisphere the left side of the body is affected. Additionally, if we look to the previous image of brain hemisphere attributes, we see that the left hemisphere is proportionately dominant with patterns-of-three and the right hemisphere is proportionately dominant with patterns-of-two. This suggests, when one takes a very broad over-view of not only the human body but all life forms if not inanimate forms as well since atoms, molecules and cellular components as well as functionalities, resemble a type of measurement. As if all such items were beads or discs on a large abacus.
There are counts and recounts of different quantities taking place in developmental biology, with some showing up more often than others and dubbed as part of a recurrence otherwise labeled as a body plan, whereby one might think of a double-entry accounting procedure as a "body plan" we might prefer to designate as a cognitive recurrence, since it is not of present linguistic currency to describe mental activity in terms of a body... plan or schematic or blueprint, etc... No doubt there are counts and recounts taking place in all terrains of inhabited and uninhabited activity. In many cases the counts re-occur like a head-count of prisoners or children on a field trip. It even appears that the Universe is counting if we can assume human perception of the Universe in its supposed "count-down" or "count-up" towards extinction or from some purported beginning is an accurate assessment based on educated guesstimation. And yet, some readers may ask who or what is counting, but it may be the case there is no one, only a mechanism set into motion by a who or what that may no longer exist, are in hibernation, or are taking a nap and are using the collective counts as a type of alarm clock.
If we put two lines together and label them as being parallel, it is also a pattern-of-two. However if we use a single line with two arrows going in the same or different directions... even opposite directions, we may not think of such an illustration as being parallel nor as a pattern-of-two, much less take the time to notice that such two-line configurations set into a frame with two other two-line variations is similar to three pairs of legs seen on insects. Indeed, the idea that human consciousness would come to reflect a similar pattern as seen on an insect is denied having parity, because humanity does not want to see itself in a light different from that illusion and/or delusion of superiority. For example, placing three different configurations of two-line orientations into the context of a subject (such as physics) labeled as an expression of superior thought, and then making other correlations to the observed patterns, may not sit well with those wanting to refuse to entertain the notion that human ideas regurgitate a similar repertoire of patterning seen on or being used by life forms or behavioral characteristics of humans themselves, that are generally not thought of as being able to express a form of sentient thought. Take a look at the following images and notice the similarity of designs being used and can thus be defined as a type of symmetry. The presence of an insect with 3 pairs of legs is a rather fortuitous addition that the original author may well have overlooked the correlation.
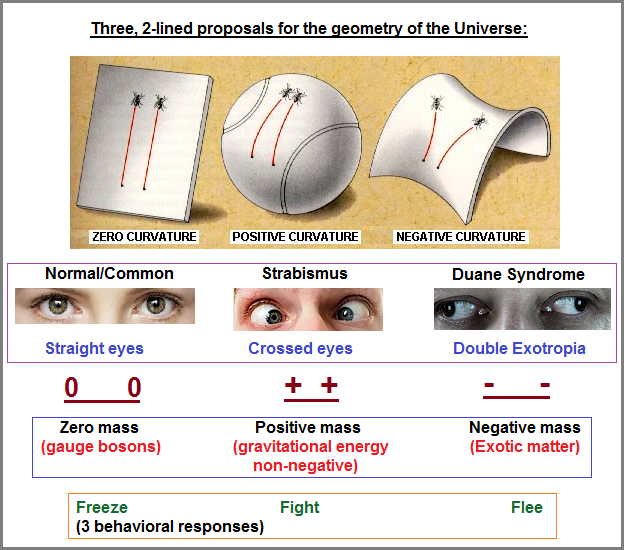
Correlating the three variables of insects, sentient thought and Mathematics, let us assume (as one example) from the perspective of spiders that they "think" the design, the geometry/mathematics of their particular species' web (whether or not their reality includes the realities of other spiders), is the foremost form of mathematical thinking in the Universe, and that any sentient being would automatically be able to recognize the brilliance, the simplicity, the beauty of their mathematics because such a mathematics governs all of existence as a Natural basic truth; but because humans can not actually understand its composition other than as a means of survival, just as the mathematics of humans is embraced as a necessity of survival and growth in many instances, humans are therefore ignorant of the utmost truth, as seen through the eyes of spiders. Humans do not routinely think of, much less teach that mathematics is a type of spider web or for that matter, a box of arts and crafts because they think mathematics is an ultimate Universal truth and not different forms of expressed cognitive webbing exhibiting basic patterns of enumeration which may well govern all of creation. The egotistical nature of humanity does not often allow humans to view themselves as dust in the wind, another brick in "the" (such as a social or cultural or species) wall. Humanity, particularly from the dedicated type of insanity pursued by those involved in some religious perspectives, are egotistically inclined to perceive themselves as a "chosen" and favoured life form by a supposed god creature. It is an hypocrisy just as rich as the one in which we find the practice of a legally binding "Jury duty" yet there is no "voting duty" nor a "government duty" to end poverty or to have term limits and many other practices of equality. It is of particular interest to note that while it is a legally binding duty of citizens to participate in the Justice system, this same supposed value is not implemented as a formula for the structure of government, whereby the idea of a "Jury Duty" system of governance would be practiced in the form of a Peoples Legislative Branch (as the incorporated Jury) and appropriately referred to as a New Government, or "Cenocracy".
The idea of Mathematics representing the highest model of thinking and that those who possess the skills to work with mathematics are superior thinking individuals, is an hypocrisy or we would require all social leaders to have erudite mathematical abilities. Likewise, we would have all professionals as first and foremost experts in Mathematics. Since we don't have such a requirement, the routine level of social thought is to permit idiots to control all institutions and sectors of society, including sports and other entertainment forms. Such people must be labeled idiots because they are not experts in mathematics. The logic in this sense is that if a person does not have an aptitude for a mathematics expertise, they are not particularly intelligent and they can therefore be colloquially referred to as an idiot.
If we continue to think that those who think mathematical are superior thinkers and thus create social circumstances which require a practiced skill in using the tool of mathematics to perform some required employment function, then a disruption in the overall social activities may well make such individuals particularly unneeded, such as in the case of devastation caused by war or disease or some natural disaster. Granted that many individuals use a mathematical-like (mechanist, that is... axiomatic) form of thinking and that the expressed formula in expressed in the task, be it a craft or some labeled art form;, that which we call mathematics and mathematical drawing in the form of an equation; is not being overlooked in this present appraisal of mathematics. Nonetheless, the conventionality of Mathematics as a particular currency of thought and expression is cherished by some as a great desirability and means by which a person, even an entire society, can gain some presumed ascendancy of thought processing in order to dominate all others within a social sphere which participates in the accommodation of using mathematics to govern the direction by which a society is to go and how it is to get there. However, this is problematic for those not wanting a person, more so an aggressive and predatory culture to gain a controlling foothold into a way of thinking which permits them to then fashion social standards in their image... so that they may come to dominate all sectors of society. To prevent this, we must move from a two-patterned dominant model of Mathematics which corresponds to a basic orientation in some cultures, to a three-patterned (or otherwise-patterned) mathematical model where such an underlying pattern is part of the cultural orientation, even if the culture is not fully cognizant of it. The whole of Western civilization must be taught that they are being subjected to a subtle attempt to be dominated by a culture wanting to exploit the present social dependency on a form of mathematics which uses a dominant (two-patterned) formulaic mindset, and therefore the existing basic patterns of thought processing need to be formalized as a recognition in order that the solidification of an other-than two-patterned mathematics will be birthed (born/created/developed).
Whereas we think that it is rather amazing for an Asian populace to train a student body to become adept at mathematics through an extensive application of school attendance as a social expectation and thus create a future population which rises to a state of assumed intellectual dominance; a closer look at mathematics reveals that a cultural orientation to the old duality concept of Yin and Yang is more easily transferred to a grasp of Mathematics which is itself exhibiting a dominant usage of dualities— than it is for a culture steeped in the usage of tripartite groupings. (Western societies apparently are more oriented towards the cultural standard usage of patterns-of-three, while other cultures are more oriented towards patterns-of-two.)
In an appraisal of Mathematics we need to look not only at the basic patterns being exhibited in the ideas of mathematics structure, but also ideas which are labeled as referents to basic models of psychological (cognitive) activity such as symmetry and archetype, along with the ideas of transition, transformation, hybridization, mutation and developmental trends which may be predictable (if we take into the Natural environmental/social conditions which will or can be artificially created to prevail (in order to insure a desired outcome or insure sustainability of an already ongoing course of events). As such, we are looking at the beginnings of a philosophical crisis of consciousness involving the usage of a particularly- patterned formula of mathematics being applied as a cultural development tool to insure a future populace has a reigning global disposition in technology and commerce, thereby affecting a militaristic takeover without ever having to fire an actual bullet, bomb, or bombastic speech.
Because the current model of mathematics being used relies on patterns-of-two variously described as dualities, dichotomies, opposites, parallels, etc., and a culture which has a history of holding a pattern-of-two orientation as a precedent for interpreting various (natural, artificialized) events and activities, we have the situation in which such a culture can implement an education requirement to reestablish an ancient orientation into a present-day perspective and rekindle a previously established cultural orientation more easily than a culture whose citizenry is brought up in a social setting where patterns-of-three are the predominant underlying cognitive orientation, regardless if a social body of people are cognizant of their inclination to think in one way more-so than another. For example, despite the philosophical analysis one might further apply to the idea of the development and design transitions of the Yin/Yang idea, it nonetheless exhibits a pattern-of-two profile that a culture steeped deeply in the presence thereof, may well make it an easier transition for many in the culture to embrace another idea such mathematics because of its dominant underlying two-patterned construction. For example, a two-patterned oriented culture will have the idea of hot/cold, whereas a three-patterned oriented culture will have the idea of hot/warm/cold. Multiples can no doubt be applied to either of these, but the point is that a culture with a two-patterned dominant upbringing are cognitively closer to learning a subject with a dominant two-patterned structure than a culture with a populace subjected to the presence of a three-patterned (or other-patterned) dominant upbringing.
It is difficult for a subject to be taught which has the requirement of learning to exercise a mentality in groups-of-two, when that subject is thrust upon a populace of students immersed in a cultural setting where patterns-of-three are the exercised cultural standard being projected by commercial interests, government practices, and academic textbook documentations reciting various important realizations of tripartition occurring in Physics, Biology, and language. Indeed, a Western cultural trend in which a population grows away from religion is an expressed example of a three-oriented culture finding exception with religious doctrines which emphasize a two-patterned thought process such as the characteristic dualities of heaven/hell, moral/immoral, right/wrong, good/evil, etc... Religious perspectives which attempt to introduce some level of significance to a position of tripartition such as in the case of the Trinity in Christianity and the Trimurti in Hinduism, are philosophical exercises which further emphasize the "two versus three" condition in that there are those who are appreciably concerned with the associated doctrines and thus indicate their mind-set has moved further afield from the older two-part traditions of thought processing.

One important realization is that when we speak of cultural orientations, a clear distinction about an enculturated mind-set and usage needs to be established. An enculturated mindset does not necessarily mean a person is conscious of such an inclination due to a repetitive emersion. In many cases the recognition of a repetition may be in the form of a particularized set and arrangement of information such as a listing of multiple three-lettered organizations which are spoken of in various media sources, or a collected ensemble of two-patterned references in the context of the Yin/Yang idea to support such an orientated consciousness. While a person with a three-patterned orientation may say they are well aware of patterns-of-two (being able to supply multiple examples), they may not be able to readily provide multiple examples of patterns-of-three. It is much like a person living in a three-dimensional world can easily see a two-dimensional landscape, and yet be unaware of how much they are affected by the three-dimensional world they live in. Conversely, a person steeped deeply in a culture where a two-patterned perspective is pervasive, even if there exists a specialized orientation towards a value of threeness, may not actively participate in an active recognition of either patterns-of-two or threes. Upon making mention of either pattern they may necessarily resort to valuing one over the other and recite examples thereof, Interestingly, I have seen criminally- (or legally) minded individuals in a three-patterned dominant culture emphasize a definitive two-patterned this-or-that articulated perception and those in a two-patterned cultural setting inclined towards the usage of a particularized tripartition actively involved with criminal activities (such as Triad gangs) or a triadically arranged justice system.
The present model of Mathematics is that which was established in an era where a pattern-of-two orientation was dominant. This "pattern-of-two" orientation is known and idealized by different names such as duality, dichotomy, Janus-effect, mirroring, opposition, protagonist/antagonist, friend/enemy, binary, bipedalism, misspoken, contrast, dimer, physics/meta-physics, nature/nurture, etc... It is not that such dichotomies are not useful, but the present model of Mathematics retains a foundation on such a pattern which is in many cases superseded by a pattern-of-three, as is appreciably recognized in biological models. This is of course assuming one wants to view Mathematics as a type of living entity instead of a non-living machine expressed as a mechanism or mechanical contraption dependent on various levers and ropes called dial-less (analog) axioms and axiomatic proofs, instead of dial-full (digital) knobs, switches and servos. As humorous as one might make the contrast without attempting to create contrasts being applied to contrasts being applied to further contrasts, the overall point is to denote we are dealing an a form of Mathematics which, by its dominant usage of dichotomies, expresses an antiquated mindset that we either need to evolve or completely replace with a new species.
One might consider that the application of electricity to an enumerated sense of off and on (zeros and ones), not only expresses a step forward in the usage of a dichotomy by making it animated, but reveals a step in evolution, as it might very well be conceived; if we also view a stagnant pairing of a zero and one as a primitive model of conceptualization. If this is the case, then an increase in speed can in some measure be viewed as a step towards a developmental expression (such as seen in cellular replication); out of which further complexity may then develop. If this is the case then the application of zeros and ones in computer language is analogous to the adopted usage of a two-patterned one and two as an exercised quantitative description when humanity first began its cognitive trek along a descriptive counting sequence with its starts, stops and transitionals. In other words, when humanity began to develop a sense of quantitative enumeration through a measure of pairing, the values of one, then two, then a third were part of the initiation process into larger quantitative descriptions of enumeration. Whereas the process was long and arduous, awaiting the human brain to come to terms with the overall idea of quantity to be represented by a vocal utterance and/or a symbol (as simple as a line in the dirt), the seriality of the 1- 2- 3... sequence was not automatic, unless of course there existed someone whose mind/brain was further ahead than their contemporaries, and by past standards, would be considered from our present perspective as being either precocious or talented, or gifted, or a genius.
Where the history of language-enumerated quantities indicates a long path until the development of mathematics, we appear to be witnessing some vestige of this scenario recurring in the language of computers. It's as if human cognition took several steps rearward in order to diverge along a different path than the one mathematics is presently on... like a cockroach, ant, and crocodile which appear to be relatively unchanged for many thousands if not millions of millennia. I speculate that enumeration in the history of humanity took place in a developmental sequence equal to the following supposition, though retreats and false starts nor leaps in conceptualization are not included, though herein noted.
- No conscious enumeration for quantity, linguistically or otherwise.
- Eventually a value equal to our present day "one" was achieved and articulated. (Did articulation precede symbol usage?)
- A value of "one" may not have been automatically accompanied by a cognitive value of more than one that was socially expressed.
- More than one was considered some value of "many", though a cultural and era-specific language may have used some other word like "heap", bunch, etc...
- One- Two quantity established.
- "Two" may have been a word initially used as a substitute for "many", but also used as a numerical specificity.
- "One- Two- Many" established as a numerical sequence. Duration of usage may have differed amongst different cultures.
- "One- Two- Three" established.
- "Three" may have been a word initially used as a substitute for "many", but also used as a numerical specificity.
- "One- Two- Three- Many"
- Etc...
This is not to say that some culture expressed some abbreviated form of the foregoing sequence, nor that some past culture could not cognitively stepped over one of more stages. However, interestingly... the above sequence looks very much like the babbling and word development stages of infancy and childhood. As if each developmental stage in cognitive expression of a physiological maturation recreates some version of an earlier staging process. Hence, the zeros and ones in computer language resemble the sequence of enumeration seen in the development of mathematics. Instead of using a doubling process as that seen in cellular division, cognitive sequencing can use a model of tripartition, though computing is following the doubling steps seen in cellular expressions of multiplication to create more complex life forms, but only one is considered to be a sentient being, even while attributing consciousness to some lower forms of life called horses, dogs, and multiple others. There is a point at which Nature abandons the usage of patterns-of-two by using patterns-of-three to create more complex forms of life.
For example, it is claimed by some that a single-stranded RNA preceded a double-stranded DNA, which is sometimes referred to as an RNA World model of evolutionary development. As yet, there is no dominant double-stranded RNA nor triple-stranded DNA. In this sense, Nature has stopped counting in this developmental theater. In Germ layer development we see complex life forms exhibiting a triple germ layer development, with more primitive life forms exhibiting a double germ layer sequencing, and a single germ layer is thought by some to be expressed by the sponges. Characteristically though, we have the concepts of triploblastic and diploblastic life forms, but no definitively named monoploblasitic examples. However, by conventional standards of observation, the sequence of development proceeds (at some point) from a single stranded RNA to a double-stranded DNA, to a 3-in-one ratio stranded protein complex. (I refer to the primary- secondary- tertiary- quaternary structures as a 3-in-one ratio since the quaternary is sometimes referred to as a composite of the three previously named forms.) Despite all the billions of years evolutionary development, there remains a retention of using small number developmental scenarios, much like the conventions of using three-patterned groupings such as (1,2,3...) and [ones-tens-hundreds (comma)] in mathematics. Though other researchers may have thought about the single and double-strand models and the absence of a three-stranded equivalent, the idea of a 1-2 -3 maturational sequence does not occur in textbook citations as an explicit.
We need a new, three-patterned dominant form of Mathematics with which a three-patterned cultural mentality is more comfortable, more adept, more in-tune with. Attempts have been made to create such a foundation from which a new Mathematics can arise, as seen in the usage of a three-part (And, Or, Not) Boolean logic set over a two-patterned (Binary- Zeros and Ones) computer code. In fact, there are efforts being made to develop a ternary (trinary) computer utilizing information from quantum mechanics based on a physics with a three-patterned foundation (e.g. three families of fundamental particles, three fundamental particles, three quarks/three anti-quarks). Whereas we have an Asian culture such as China practicing a "long view" philosophy of wanting to dominate all other cultures by way of rigorously instructing a population of students in the rote learning of a type of mathematics presently being used the world-over to direct the activities of all government, commercial and scientific explorations; they will fall short of this goal to gain a total dominance if other cultures adopt a new type of mathematics which does not pre-imminently rely on dichotomization due to antiquated axioms from which mathematical formulas are both erected and solved.
Humanity will stagnate with the continued usage of an outdated form of mathematics, despite one or another culture succeeding to develop a populace where a larger majority of its citizens are adept at mathematics, thus winning mathematical awards for an assumed excellence in thinking; whereby the pursuit of applying such a mathematics ability to accepted standards of present social activities gives the impression and advantages of creating a dominant culture that all others must kow-tow to as if in the presence of an emperor, despite a country calling itself a form of "Democracy" (or peoples government).
This is of course unless some type of "punctuated" or "exclamatory" event doesn't thrust itself upon the consciousness of humanity to a degree that civilization becomes caught up in a whirl-wind episode of development which human cultures are not prepared for— because, despite all the avowed imagination and alternative proposals made within the domains of the different subjects humanity has become involved with both personally and commercially, humanity may not have had even a miniscule glimpse of a possibility that is erected as a bridge which must be crossed over or lest humanity perish; as all its efforts appear to presently be on a course for, if we are to deduce our conclusion based primarily on models of thought influenced by motion pictures portraying variations of an Apocalypse, reinforced by many specialized religious perspectives from which the word Apocalypse is derived but has been transformed into a general theme of widespread and lasting destruction of human civilization and the overall species itself. However, the incremental deteriorations of the Sun, Earth and Moo's current viabilities for helping to sustain life are in accord with the idea of an ultimate demise.
In the above sense of retracing the roots of mathematics by way of using mathematics as a tool to unravel basic patterns, we are using the dichotomy of stepping backward to go around the obstacle of dichotomization in order to make a forward gain. While this at first may appear to be hypocritical to those who are familiar with the widespread usage of dichotomies in mathematical processes, it is necessary at this juncture in the discussion so as to invite dichotomously-minded individuals to find some modicum of familiarity, since to start off with a trichotomic orientation may dissuade such users of dichotomy... particularly those who are not aware of their top, bottom or middle-heavy usage of dichotomization. In other words, the idea of stepping back to go around an obstacle in order to make a further forward gain is easily understood, but may not be to those who are not familiar with looking at words, sentence structure and application in basic numerical terms. Let us take for example the phrase "Home Sweet Home". It is a singular phrase with the repetition of two words conjoined by a third, whereby referencing it as three-part phrase may be easier for some to appreciate. It is not that there aren't shorter and longer phrases words and other parts of speech can't be counted, but that such a process of counting is (apparently) not a typical exercise for most people. (I say "apparently" because I do not know most people, but that those I have encountered have not made any attempt to introduce such an idea in a conversation.)
The notion of "stepping back to go forward" may be the central idea someone focuses on and therefore indicates they may have a preference for dichotomization, even though the third idea of going around an obstacle is part of the view. Hence, I refer to it as a dichotomy (as an exercise in advertising), though it actually is a trichotomy which can now be seen by some readers as denoting dichotomization as the obstacle, and will be made more clear as I continue.
In my view, Mathematics is stagnant. It is non-dynamic, even when attached to moving processes... like a turtle on the back of a scorpion trying to ford a stream or attached to a field of research giving the impression of movement such as 'fluid dynamics'. Whereas we have enjoyed the development of alternative mathematically labeled branches, the tools they are using are not new. The numbers are the same numbers despite attempts to be presented as being something original by applying the tactic of introducing some dual characterization like rational/irrational, or real/imaginary, subscript/superscript or fraction/whole. Cutting a fruit in half or in any proportionality that is differently named/labeled, does not alter the state of the fruit as if to make it a vegetable or some animal. How the old tools are being applied to new problems is not to be disputed, nor that such tools can be uniquely wielded by the crafts-people of the different models of tools already in existence (e.g. geometry, trigonometry, algebra, calculus). Yet, each of them is stagnant. To take but one example being used as a comprehensive referent to all of Mathematics, we need a new Calculus which is dynamic, and not merely being claimed as such by way of its application to moving subject matter. Hence, like an Accordian in motion, let us attempt to visualize the development and usage of an Accordian Calculus.
To claim that one or another model of Mathematics is dynamic because of its association with subject matter that is in motion, is like claiming nail polish is in motion because it is place on fingers which move. This is how so very much of mathematics is used— as an embellishment, as a decoration, as a means to highlight and emboss some particularity of interest or concern to create an impression and appearance that would not otherwise be seen nor added to the repertoire of humanity's hunger for projecting an otherwise vapid egotism with a voracious predatory hunger. By way of analogy to disclose the character of mathematics' present state of existence, one might use multiple models to express it primitive state of development which is not being permitted to evolve, but instead forced into different niches which solidify one or another type of development to retain a particularized developmental scheme. In any respect, we are looking at a recurrence of primivity that is regenerated to produce generation after generation after generation... the same cyclicity of regurgitated growth, producing little more than a re-imaging of a sustained primivity which act as organisms that become studied by separate specialists like Anthropologists, Archaeologists, Anthropologists, Ethnologists, Sociologists, Zoologists and others... studying on remote islands or remote habitats, all claiming that their efforts are needed and must be taught as part of a curriculum to force more and more information into the media saturated brains of the public. Imagine if you will the state of affairs if all the life forms which Nature has ever developed were abundantly visible for examination in one respect or another. How so very large an Encyclopedic mind would be the focus of education to create in order to make an assumed better world by creating a civilization where everyone shared the same amount of knowledge, and yet different religions and businesses and governments wanted to emphasize their own value to which all the knowledge should be directed so as to fulfill the motivations of individual leaderships.
Analogously, mathematical "craftsticians" are nonetheless akin to the skills of those who have been brought up with developing a facility for using the abacus in contrast to a pen/pencil and paper method, though both of these can be supplanted by the usage of a calculator when the complexity of problems is increased. In a different but similar sense, changing a math exercise from a symbol to number to a color toy puzzle does not create a different cognitive toolage, only how the old tool is applied to different contexts. Each of the following examples can be viewed in terms of a horizontal- vertical- diagonal spatial orientation, whether or not this is openly articulated. A person can visually see they have options along these three directional paths, though they may only choose to use a dichotomy or singularity due to some frequently used course of action. The usage of Dichotomies instead of Trichotomies is an habituation, is a mindset which many use such as in terms of back-stepping, sidestepping, retracing steps, circularity of approach, stop and go, etc... This too is the strategy we can see being used by mathematics as a resorted to preference, but is cloaked, is shrouded, is camouflaged by application and the disguises used by cultural standards of accommodation such as with words like tradition, holiday, vacation, break/lunch period and the like. So too is such an habituation concealed both in commerce, games of chance and intellectual exercises such as chess, billiards and checkers, where geometry and other mathematical indices abound.
(continued on next page)
Date of Origination: 19th March 2022... 5:23 AM
Initial Posting: 8th August 2022, 9:10 AM
Updated Posting: 2nd January 2023... 10:57 AM