~ The Study of Threes ~
http://threesology.org
Visitors as of 2/27/2021
Note: due to illness and a computer whose hard drive and fan went out at the same time, and no ready backup-files method was being used, I lost my place (line of thinking) during the recovery and rehabilitation process and will at sometime have to redo this Series on a Static and Dynamic Calculus. For good or bad, I can not recover the frame of mind which intensified my energies when beginning the project. I am having to retrace my steps on several different pages in an attempt to collect what I was thinking while writing them since information on the old hard drive are as yet irretrievable due to a busted read/write head. Apparently, while under the throes of illness, I created pages that, upon re-reading them, seem rather... let us say poetically or artistically adventuresome... though I sometimes prefer to consider as momentary bouts of illness-induced playful madness.
In our efforts to pursue unadulterated "truth" in pure and applied mathematics, it must be noted that current mathematics is being adversely affected by the social environment it is being subjected to in all cultures, due to the atmosphere of a profound lie being perpetrated by the exercise of political philosophies claiming to be an effort to maintain or develop a full expression of Communism, or Socialism or Democracy, or some mixture thereof. The widespread aura of a lie is being thrust onto the publics of the planet Earth forcing them to negate their developing consciousnesses to perceive a more valid reality, by engaging in illusions, delusions and in some cases, psychotic formulas of thinking to defer themselves to such illegitimate standards of orientation. Because we are brought up to believe that we are involved in a society which pursues a greater exercise of equanimity and necessity for the good of one's nation, we obligingly create a working hypothesis for accepting a government's claims of political righteousness. Nonetheless, whether one thinks they live in a culture where their government is attempting to create a "best fit" ideology for given circumstances prevailing at a given time in a given era; the truth is that such a practice affects all those who are under its auspices, since they must alter their thinking so as to oblige the dominant orientation, and thus transfer this obligated agreement to their work routines, habits and results.
By way of an analogy: If one tries to construct a dwelling under the auspices of an entity whose rules and regulations are so laborious as to resemble a maze, if not gauntlet; one's behavior and thinking must obligingly do as is required and alter their plans to fit within the codes created by those who may not permit an allowance for exceeding the standards of the code. And this is the case with mathematics and other genres of human activity. One can not offer an exception which provides for a step beyond the conventions of thinking unless one abides by standards of description which prevent one from exceeding those conventions. A case in point is when a building code calls for a 2 inch by 6 inch board to be used and one wants to use a 4 inch by 12 inch board instead. The more sturdier board can not be used because it is not "up to" code. Codes, just like axioms in mathematics, do not provide an allowance for practices which are not in line with a code because they exceed the standards of a code. It is like living in a police state of intellectual activity. Where one is permitted to behave in accordance with laws which have been allocated as proper, patriotic and perfectly normal, but are not permitted to exceed such standards unless they occur in an isolated setting where the presence of a given officer permits alternatives to be expressed, even though they do not conform to rules which are meant not only to obligate restrictively, but ensure everyone "stays in line". While academicians may well provide for the allowance of alternatives amongst themselves, and may be able to provide adequate reasons for allowing an exception; they still retain the ability to negate such an expression and even define it as being absurd, if they feel they are in someway being slighted by the exercise or the person(s) engaged in the exercise thereof. Allowances are policed very closely as well. Those whose activities are being questioned by the expression of someone's alternative view, receive greater scrutiny. If the alternative view can not be seen as providing a reward to those who guard and perhaps develop standards, they may well reject any claim by a would-be usurper.
My view is that the word "Mathematics" is the label of a box in which is kept various arts and crafts. Some of the items are interesting to look at and others have been adapted to serve more practical uses. Because it is a box, like the titles of so very many other boxes (biology, physics, music, philosophy, architecture, anthropology, archeology, medicine, engineering, toy, shoe, fishing tackle, tool, sewing, computer, etc...), attempting to describe a better model of mathematics requires one to realize they are in fact dealing with a circumstance which can be relegated to the perspective of not only being a box, but those who are adept at using the arts and crafts inside the box, are not necessarily adept at understanding that in order to think or even see outside a given box, we must come to some appreciation of what type of box it is. This is a necessity because the type of box we think we are dealing with will determine how we come to think about cognitive approaches outside the box (for example, its parameters). If it is a round box one is speaking of, then thinking outside its contours will determine the line of thinking we pursue in accordance with. Likewise if it is a square, tall, cylindrical, abstract or alternatively named box such as a cookie jar, bread box, ice box, shoe box, ice box, sewing box, cigarette box, cigar box, junk drawer, lunch boxing (sexual reference to oral sex with a female), cigar box, bottle, pack, package, test tube, wrapper, etc... Even though we may attempt to circumvent such an entanglement of considerations by adopting the view that one word or symbol can be used as a generality (for example the words container, containment, perimeter, enclave, niche, shelf, drawer, cabinet, etc.), such even though such views are yet another type of box, (which frequently involves using the three-letter word "etc.", to express multiplicity in terms of a proposal suggesting infinity. (A statement can be a cognitive box about one or more boxes.)
Yet, not only does mathematics reminds me of a box of arts and crafts, but a toy box of different games. And some people play the different games quite well,
much like we see some people being able to perform a Rubik's Cube, shoot billiards, play tennis, etc... "Mathematics" just happens to be the label on the box
which some people have learned to accommodate into their lives to the point of using it to make a living. I am not such a person. In fact, admittedly, I am not
very adept at mathematics but I see it for what I believe it to be. No less, because of my interest in what I call the "threes phenomena" occurring in multiple
subjects, I use mathematics in terms of a simple counting theme. Others such as those interested in Numerology also take part in a counting effort by cataloguing
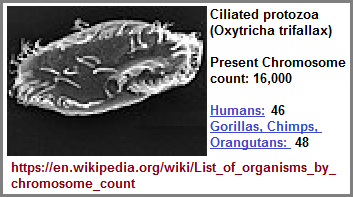different examples of ideas and occurrences involving different numbers, but rarely do you see a Numerologist making reference to the fact that the overall
sampling of numbers is extremely limited in comparison to the many numbers humans have at their disposal. It is the same case for what are termed Natural laws
and natural events, such as the three families of fundamental particles, a triplet code in Genetics, as well as a three-divisioned Pentadactyl vertebrate
skeleton. There are of course other number patterns but the point to be made is that with only a handful of exceptions, do we find the usage of larger numbers
such at the 16,000 chromosome count of the volvox virus (List of Chromosome counts) and the 26,000 year cycle noted in the Orbital
((Milankovich cycles)
variations.
The Earth system has undergone a general cooling trend for the past 50 million years, culminating in the development of permanent ice sheets in the Northern Hemisphere about 2.75 million years ago. These ice sheets expanded and contracted in a regular rhythm, with each glacial maximum separated from adjacent ones by 41,000 years (based on the cycle of axial tilt). As the ice sheets waxed and waned, global climate drifted steadily toward cooler conditions characterized by increasingly severe glaciations and increasingly cool interglacial phases. Beginning around 900,000 years ago, the glacial-interglacial cycles shifted frequency. Ever since, the glacial peaks have been 100,000 years apart, and the Earth system has spent more time in cool phases than before. The 41,000-year periodicity has continued, with smaller fluctuations superimposed on the 100,000-year cycle. In addition, a smaller, 23,000-year cycle has occurred through both the 41,000-year and 100,000-year cycles.
The 23,000-year and 41,000-year cycles are driven ultimately by two components of Earth's orbital geometry: the equinoctial precession cycle (23,000 years) and the axial-tilt cycle (41,000 years). Although the third parameter of Earth's orbit, eccentricity, varies on a 100,000-year cycle, its magnitude is insufficient to explain the 100,000-year cycles of glacial and interglacial periods of the past 900,000 years. The origin of the periodicity present in Earth's eccentricity is an important question in current paleo-climate research. ("Climate change." Encyclopædia Britannica Ultimate Reference Suite, 2013.)
When we look for repetitions of larger numbers in different subjects, we do not find them being exhibited as we do small number patterns such as ones, twos, threes, etc., though different labels such as Uni-verse, Singularity, dichotomy, Triune, etc., may be used individually or in sets. The usage of the word "Plurality" appears to be used as a "Many" reference found in early counting systems which described larger quantities beyond simple (such as one and two) points of cognitive demarcation. In other words, larger numbers appear to play the primitive cognitive part of "many" (or much, a lot, more, bunch, heap, etc.)
It goes without saying that mathematicians are counters, though a different breed of counter from the activity of a business accountant, but both nonetheless rely on some form of double-entry accounting method. The double-entry account method is just a different model of the recurring usage of a dominant orientation towards dichotomization, which infects all subjects which rely on mathematics as a standard by which an attempted uniformity is sought after in practice. And it is this reliance which I will attempt to point out as being extremely problematic, albeit having a usefulness so long as humanity retains an orientation for perceiving the world in a two-patterned fashion of even-number doubling, overlayed with the usage of a three-patterned odd-number trichotomization which can provide for recurring types of differentiated balancing acts such as the trisomies of genetics, triads found in religion, and the multiple triadic structures found in a multiple of cognitive exercises together with ensembled patterns which mix and match odd and even number patterns such as for example the "2-3-4" pattern with examples found here: The Devil's Advocate page 14.
Humanity's early counting schemes has led us to the present facility of mathematics we have come to align our human civilization with to draw experiences from perceptions of the past, present and possible future that may come as a result of such an alliance and reliance. The counting scheme phrase of "One- Two- Many" is a generality that can be used to describe humanity's early counting efforts, where... in whatever language equivalent way one's era used in communication or self orientation to perceived reality, there came a moment when the concept of "1" came to be consciously recognized by way of pairing quantity with a symbol that may have been little more than a notch on a piece of bone, a grunt, or some gesture. All other quantities were possibly viewed in the established language equivalent way of being "all the rest", many, much, heap, etc... In other words, there was an expressed cognitive limitation having been reached, though there may have been those who were individually ahead of all others in their social sphere. Then, one might assume... the mental trek towards a "2" quantity arose that experienced another cognitive stopping point, with all other quantities beyond the "two" being viewed with some language equivalent many, much, heap, pile, etc... This is not to say that all people experienced the same cognitive limitation since their may have been exceptionally intelligent (number oriented) people living among those having difficult grasping any model of number referencing ability at all. While there may have at some later time been an "explosion" in the cognitive conceptualization of quantity, the usage of the three-patterned phrase "one- two- many" can suffice to illustrate all early number-related counting methods. I say "number-related" to make note of the presumed counting abilities of animals who may not "intellectually" or mentally use a number system to count with, but nonetheless exhibit behavior thought to be reminiscent of human counting.
The method of counting by human might be interpreted to be multiple types of counting because of the usage of different items and symbols employed by different cultures such as shells, rocks, sticks (etc.,) as well as different mediums (stones, bones, clay tablets, etc.,). Whereas one might claim or infer that different cognitive methods were employed, let us instead simply say that only one model of cognitive activity was used and adapted to the environmental setting in which they occurred. If rocks or bones or seashells or leather, etc., was the preferred medium used for tabulation, this does not mean different types of counting were used. And even if one prefers to say that different cognitive methods were employed so as to defer to those who think human imagination is not limited, the fact remains humanity has ended up with a singular types of mathematics governed by a given set of axioms with individualized counts for different mathematical orientations such as:
In some orientations we need not have multiple axioms but a singular axiom which represents a collection of ideas thrust together in what may at first appearance exhibit an illogicality, but upon closer examination reveals a circumstance of choice:
(Axiom of choice) sometimes called Zermelo's axiom of choice
(Axiom of choice is a) statement in the language of set theory that makes it possible to form sets by choosing an element simultaneously from each member of an infinite collection of sets even when no algorithm exists for the selection. The axiom of choice has many mathematically equivalent formulations, some of which were not immediately realized to be equivalent. One version states that, given any collection of disjoint sets (sets having no common elements), there exists at least one set consisting of one element from each of the nonempty sets in the collection; collectively, these chosen elements make up the "choice set." Another common formulation is to say that for any set S there exists a function f (called a “choice function”) such that, for any nonempty subset s of S, f(s) is an element of s.
The axiom of choice was first formulated in 1904 by the German mathematician Ernst Zermelo in order to prove the "well-ordering theorem" (every set can be given an order relationship, such as less than, under which it is well ordered; i.e., every subset has a first element [see set theory: Axioms for infinite and ordered sets]). Subsequently, it was shown that making any one of three assumptions enabled one to prove the other two; that is to say, all three are mathematically equivalent:
- The axiom of choice.
- The well-ordering principle.
- Zorn's lemma.
The axiom of choice has the feature–—not shared by other axioms of set theory–that it asserts the existence of a set without ever specifying its elements or any definite way to select them. In general, S could have many choice functions. The axiom of choice merely asserts that it has at least one, without saying how to construct it. This non-constructive feature has led to some controversy regarding the acceptability of the axiom. See also foundations of mathematics: Non-constructive arguments.
The axiom of choice is not needed for finite sets since the process of choosing elements must come to an end eventually. For infinite sets, however, it would take an infinite amount of time to choose elements one by one. Thus, infinite sets for which there does not exist some definite selection rule require the axiom of choice (or one of its equivalent formulations) in order to proceed with the choice set. The English mathematician–philosopher Bertrand Russell gave the following succinct example of this distinction: "To choose one sock from each of infinitely many pairs of socks requires the Axiom of Choice, but for shoes the Axiom is not needed." For example, one could simultaneously choose the left shoe from each member of the infinite set of shoes, but no rule exists to distinguish between the members of a pair of socks. Thus, without the axiom of choice, each sock would have to be chosen one by one—an eternal prospect.
Nonetheless, the axiom of choice does have some counterintuitive consequences. The best– known of these is the Banach-Tarski paradox. This shows that for a solid sphere there exists (in the sense that the axioms assert the existence of sets) a decomposition into a finite number of pieces that can be reassembled to produce a sphere with twice the radius of the original sphere. Of course, the pieces involved are non-measurable; that is, one cannot meaningfully assign volumes to them. ("Axiom of choice." Encyclopædia Britannica Ultimate Reference Suite, 2013)
Let me reassert that "patterns-of-two" play a large role in Mathematics, and like the binary code of computers, a three-patterned Boolean logic (trinary code of And- Or- Not) is superimposed over it as an intellectually created form of camouflaging it presence as a dominant characterization of a thought process that I view as an example that humanity has retained a very primitive counting system as the formula of generation for all later mathematics. It is so heavy an implement that it acts sometimes as an anchor for further mathematical development and at other times as a "sink" (think heat-sink). The properties of light known as reflection- refraction- absorption are a good analogy to the present usage of mathematics. In short, present mathematics is static, and not dynamic, despite its application to movement such as in fluidic properties.
Whereas counters of numbers such as found in typical numerology settings are themselves exercising a static orientation of repetition due to exhibiting a small quantity of examples from a small quantity of subjects as being representative of what may otherwise be thought of as a "many more available" quantity, it should be realized that my own efforts are directed towards a larger assemblage of the different number patterns (and associated other patterns) to be found in different subjects, even if a given author or researcher uses words or symbols instead of numbers to express quantity. I am dealing with sets of individually different numbers as well as an overall set of all the numbers collated together as a representation of human cognitive behavior constrained by the present usage of a mathematics orientation which relies heavily on a two-patterned foundation, much in the manner as ancient Chinese relied on a two-patterned yin/yang disposition.
Indeed, one must think in terms of statistical probability when it comes to finding a recurrence of a given number as a pattern of expressed cognitive activity and realize that amongst all the possibility of numbers, we are dealing with a representation that seems rather improbable, unless we are using the incorrect type of mathematics in our efforts to arrive at some semblance for understanding why all of Nature appears to rely heavily on the recurrence of certain low number variables being repeated. For example, instead of a million coding system in DNA or a recurring developmental (Evolutionary) trend whereby the triplet code advances towards a larger number, and along with it the quantity of atomic particle families beyond the value of three; we are seeing low quantity variables being stagnant. If this is not the case due to an imposed survival mechanism in an incrementally deteriorating circumstance, we need to find another reason for it and not brush it aside as some fool-hardy exploration.
The question also remains of why humanity apparently used only one type of counting system in the establishment of the current form of Mathematics, even though some readers might argue that Mathematics is varied... all the while they are using the same type of underlying mathematical process! Whereas in fact the counting method I am employing for dissecting different subjects may in fact be a different counting formula from which can arise a different model of mathematics which is not confined to the current static orientation, thus representing a dynamic mathematics model.
Some people are so consumed with maintaining a level of competency for keeping their respective place in a given box, they have little time to even consider thinking outside of it, unless "outside" is a designated allowance such as a short vacation, holiday, or other social activity dependent on one's perceive social or academic or work-place position within a given box.
If I present you with a Rubik's cube and call it a box, or a chess board and call it a box, or a strand of DNA and call it a box, do we not approach these different boxes in a different way, if we so desire to imagine we can begin to think outside them... or beyond their design? Similarly, how does one think of a different color if they are largely immersed in only one or those of the rainbow, if it is the custom not to mix them? How does a mathematician know what I am talking about when I describe a difference between a static and dynamic equation, if their understanding of the words differs appreciably from mine, since they are inclined to use such words in accordance with how they are used in the box of mathematics, while they are busy with one or another art or craft there in?
Typically, equations don't move and are therefore static. The idea of movement when applied to an equation is that it represents a still picture of movement, just like when we take a picture of a soaring bird, jumping fish, falling leaf, etc... While equations found in Calculus are static representations expressing movement, they themselves do not exhibit movement unless we print an equation on a piece of paper and fold it into a paper airplane or carry it around in our pocket. The distinction of what is meant by a dynamic equation and an equation which is dynamic or dynamical, is not typically considered to be a worthwhile topic to ponder in terms of moving mathematics beyond its present state of static-ness. This is due to the fact that we humans, for the most part, do not actually understand what mathematics is in terms of a cognitive activity related to other cognitive activities such as language. Indeed, because it appears that some birds can count without using language... at least not in the sense that we humans do... we are confronted by the issue of whether some sense of enumeration arose before language. If our brain was able to recognize quantity before language was developed (though not necessarily all vocal utterances), then we are confronted with the real possibility that our present mathematics is a precursor to a "higher" cognitive activity either awaiting in some shadow, or attempting to establish some semblance of a fledgling expression, but established mathematical traditions expect the human brain to be trained to carry out its activities in the current shape of the mathematics box.
Let me approach my perspective from another way of illustration. Several decades ago while at a meeting involving numerous teachers, administrators and at least one psychologist, we were collectively asked to participate in a group exercise. Several people were assigned to (masking) tape out a square box onto the carpeted floor in which all of us were asked to get in it. We were then asked to get out of it. Then slowly the taped box was made smaller and everyone was asked to get into it. Again, the process was repeated, and it was generally thought (except for myself it seemed), that we were expected to close quarters in order to keep getting into the decreasing box. Although no one gave us any direction to keep getting in and out of the box each time, several of them assumed this was the case and everyone else followed suit. The square got so small that people were literally standing on one's another toes... except for myself. My immediate supervisor very sternly directed me to get into the box like everyone else, but not everyone was in the box. The administrator directing the exercise was not in it nor his assistants who had done the taping. It was clearly stupid to be like everyone else, but as I looked at the faces of the bunched-up crowd, they were literally vying for the best position in the group, as dictated by the constraints of the box.
If you carve out a niche' for yourself in a given box, you may do well depending on where the box is situated in accordance to the position of other similarly shaped boxes. If there are only so many positions in a given box and you have more people than the box provides positions for, those who don't acquire a spot must seek out some other type of box (social/academic/employment... etc.,) in which to apply themselves; though this does not mean they are actually spending any measurable time away from the 1st, (or 2nd or 3rd) box that they hope at some time to be a part of. While they may not be physically in the box, they mind longs for a plays there in and thus keeps them from applying themselves to thinking outside the box in a genuinely original way.
Is it possible to provide an insight into the development of a dynamic calculus, if that type of calculus expressed a perception which "moves" past the contours of the typically used calculus structure? Let me give an alternative example. Years ago while working with two others, the supervisor presented me with a puzzle that was easily discernable as a dead end syllogism. A type of chicken and egg situation that one need not spend any appreciable time on. When I expressed the problem's solution with a shoulder shrug, the other two employees spent the rest of the morning discussing alternative courses of cognitive approach. Even though I insisted the problem was a dead end, all three of them thought it meant that I was providing an excuse because I couldn't answer it. There was no answer, no matter how hard one wanted to think there was. And this too is calculus. It is an answer to itself. To calculate calculus as a calculable entity unto itself, one must realize it is a craftable art with different applications, but does not render itself readily available to providing and answer of what lays beyond it. This is because it has been contoured to fit within the reality of a box called mathematics. A mathematics which is contoured by a given set(s) of rules and processional order like packages running along a conveyor belt. However, in order for the whole of mathematics instruction to change, the realization that it is an arts and crafts box must become a socialized cognitive reality. In short, mathematics must be taught as an arts and crafts program.
Even though some people take their art and/or their craft seriously, there is too much seriousness being applied to the instruction of mathematics, given the situation it is being taught like a must-have-it-to-graduate course in Latin. Yes, that's right. It is being taught like a language that is not only foreign to the cognitive reality of many people, the application of many mathematics courses to the practicality which most people will be confronted with, is simply worthless... no matter how many academicians claim that it helps people think better, more logically. Such logic as described by mathematics is not routinely translated into a common vernacular used for communication. When there are far too many people achieving high paying positions who do not have a defined "mathematics" background and interact with the young, the so-called useful logic of mathematical reasoning cannot help but fall on deaf ears unless we as a society make it a requirement that all people in all positions exhibit a thorough understanding of basic and higher mathematics or they can not get a job. The problem is, we have too many intellectuals who don't want the entire public to be equal with themselves or they might them be faced with such a level of competition they would not be as employable or as smart as they think they are. There is so much stinkin' arrogance and egotism in so many human endeavours, there exists a concerted effort on the part of how society is fashion (as a box) and maintained to ensure that multiple many people fail. Indeed, all too often one can be confronted with a situation in which a person is set up for failure in order to make another person feel they are superior... like so many on social media who try to entrap someone in a conversation only to provide themselves with the impression they are more intelligent.
If we made basic and advanced mathematics a deliberate criteria for getting a job, most of the work in society wouldn't get done. If everyone had the same mathematics background, we would have a society where everyone might well think themselves too intellectually superior to do any menial task. Along with mathematics and many other academically designed badges is an arrogance that gets more and more difficult to see when everyone in the same room expresses the same unrecognized level of arrogance... including an arrogance of who exhibits the greater humility! So where does this leave us when attempting to convey the idea of an existing type of cognitive orientation involving the difference between a static and dynamic model of calculus? If calculus or any model of mathematics is viewed as the foremost type of craft and to do exhibit something more profound requires the application of yet another block to the conventionalized pile, how can humanity prosper if it is being held back by that which forces it to maintain a given level of functioning around which society revolves and creates multiple positions where individualized forms of arrogance are permitted to be exercised?
Do we await some global plague or catastrophic war to remove the obstacles, whereby a new orientation can come to the fore like a revolution allowing for the introduction of a new form of government that was not enabled to rear its head because the former government aligned itself with those and that which helped to maintain the system of reciprocity? For example, although the U.S. Declaration of Independence clearly states that the people have the right to overthrow the government and create a better one, this is not the case as attested to by the arrests of those who, in 2021, waged a protest at the U.S. Congress but have been cited with those attempting an insurrection. Granted there was no central leader and no actual pronouncement listed grievances against the government avowing to an attempt to change the government, the simply fact that a small portion of the public engaged in such an activity is not viewed in proportion to the allowances made in the Declaration. It is an hypocrisy, just as much as it is an hypocrisy to expect a cognitive view of Mathematics beyond current conventions to exercise itself in a manner equal to that which it is voicing an opinion to step beyond! It is much like stating that if a person survives a dunking (drowning) while tied to a chair they are innocent and if they survive the drowning they are guilty and therefore are in league with the devil. This is how I view the present state of mathematics. Mathematicians allow for a view beyond mathematics so long as mathematics is used to convey it!
I am permitted to describe an unconventionalized view outside the box of mathematics so long as I use conventionalized mathematics to describe the view! This is like permitting someone to be better than a player in a given game so long as the player plays by the same rules of the game... and not allow the creation of a new game where no one inside the conventional game has established a controlling position. Proposing to change the game of mathematics is not permitted. There are too many people, too many positions, and too much money involved with the game of mathematics as it is presently being played..
We have not only fashioned our society around a working model of mathematics, but have fashioned our mathematics around a working model of society. Unfortunately, the social model is faulty and therefore requires that we prepare mathematics for the changes up ahead. A predictive model is warranted.
For example, it is well known that the present so-called "Democracy" of the U.S. is but one flavor of many others. In this sense, all flavors are phony in that the idea of a supposed "Democracy" as a "peoples government" is a false, ideological box. If the U.S. and other so-called democracy flavors were actually "peoples" governments, then the practice of a jury duty model (Peoples Legislative Branch) would be practiced. Since having a jury of one's peers is viewed as a good, if not great feature of a Democracy, then a government fashioned on this ideal state should be written into any and all models of Constitution (whether written or not); which is far superior than the present "Representative" model where the average man and woman are not enabled to run for an electable office because of party, financial or other commercialized restraints. An actual "jury duty" form of representation requires the allowance, nay, the Constitutional provision that any man, woman or worker be permitted to run by way of a process that is not a contrived labyrinthine political structure nor one dedicated to allowing selection to be determined by any selective person or entity wanting to stack a jury with those who promise to be profitable for their views. Hence, while the words "jury duty" are used, this is not to convey the idea that the current jury duty selection process is to be used for creating an actual peoples legislative branch.
Let us refresh the previous point by providing an alternative view that exemplifies the situation about mathematics being contoured by the social structure in which a given mathematics orientation is applied. Social circumstances can alter the types and teaching of mathematics and therefore restructure the box in which mathematics inhabits. A case in point is the "fudging" of numbers on a tax return to achieve a desired result, unless one uses a non-mathematical approach such as refusing to feel out a tax reform and pay taxes. While there are set rules in mathematics, there are those who are likewise set on a course of trying to circumvent the rules, like some lawyers seeking out a loophole if "creative accounting" did not work so well for a client found guilty of a fraudulent return.
Another flaw in the current structure of the mathematic's box is its symbiotic habit of allowing itself to be used by a society in which the claims of its military being part of a democratic process is actually an hypocrisy when one looks at the Military as a stated Socialist and Communistically run enterprise. to give but one example from the following list, we find that whereas it is believed that voting for one's leaders is a distinct quality of a true democracy, the fact that enlisted personnel are not permitted to vote in their leaders is a telling point about the entire organization. Indeed, when does a supposed country like the U.S. with its avowed "Democracy", need the assistance of a non-democratically run institution like the military to support it? The allowance for such an hypocrisy is a tell-tale indication as to the state of our current mathematics and other genres of serious study.
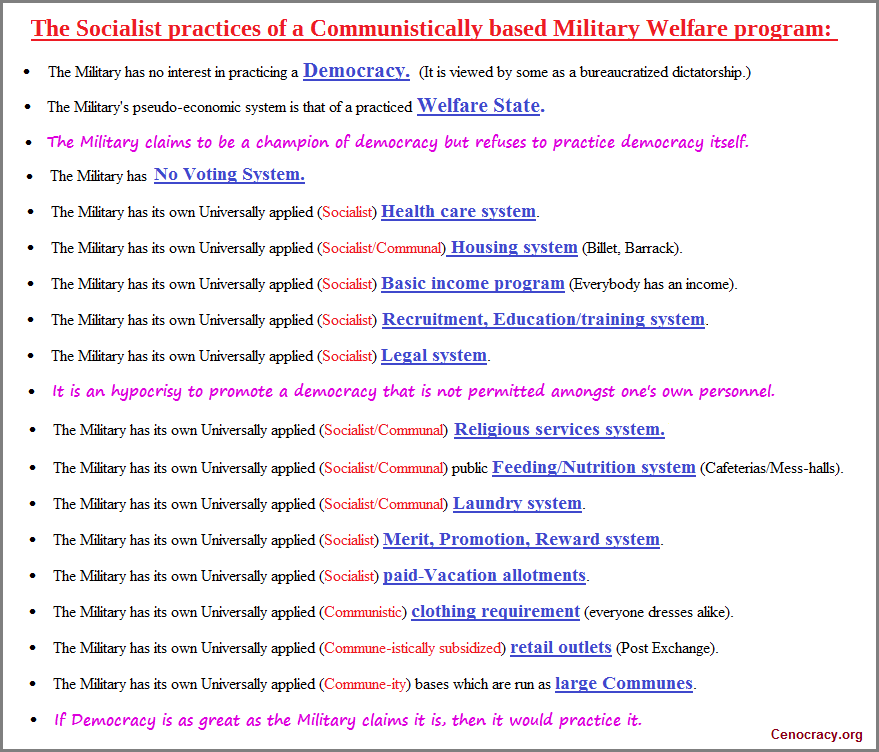
It is said that history is written by the victor. Let us add that the type of mathematics being permitted is also due to the acceptance of the victor being convinced by mathematicians as to the need for their craft... or at least the innocence and non-threatening activity it poses. Since many a mathematics orientations have been used to qualify a given perspective, right or wrong, it is of need to be routinely suspicious of mathematics and not take it at face value. It goes without saying that we can easily "fudge" equations to fit our predispositions. Yet to claim that this is the case requires more than merely showing correct equations or proposing an advanced equation within the guidelines thought to be second to no other kind of logic. One must correct the perspective from which the particular mathematics is derived by reviewing basic patterns and denoting those patterns as having a similarity to other patterns found in other genres of thinking, so that the translations of ideas into numbers and symbols can be reversed to indicate flaws where they might exist. Using mathematics alone to investigate mathematics is a fool's errand.
Date of Origination: 7th January 2022... 5:30 AM
Initial Posting: 7th January 2022... 10:06 AM
Updated Posting: 18th March 2022... 12:47 PM