~ The Study of Threes ~
http://threesology.org
Visitors as of 5/275/2021

In an attempt to discuss what is or is not the language of Mathematics, we are confronted with perspectives of whether Mathematics is an art or a science, as well as whether Mathematics (is) Invented or Discovered?. Both such references point out dichotomies similar to the Nature versus nurture controversy, and can be counted as one of several Persistent Dichotomies. The acknowledgement of recurring dichotomices in mathematics is part of the language we see in equations, but is not being placed into equations as a variable.
Many people use language to count with and likewise count particularities of language found in the idea such as grammar. For example, we say that a noun is commonly referenced with three examples noted as Person- Place- Thing. Or we say there are two genders labeled Masculine and Feminine, though some include the notion of Neuter, to bring the count to three. Mathematics, albeit it on a simple number usage scale... is being used to quantify... though less commonly used to identify the recurrence of an ongoing limitation be expressed by the human mind and nature. For example, DNA has a triplet coding system. It does not have an infinity count nor some lesser value such as a 3 thousand count. Though some refer generally and generically to the human genome as having 3 billion base pairs (Human Genome Project FAQ), they may think this is a lot and not an expressed limitation nor as a list of patterns-of-two. Nor do they typically cite the 23 base pairs in a human chromosome as a correlation to the 23.5° tilt of the Earth's axis (as an environmental effect on establishing the "23" quantity); with a doubling of this resulting in 47 (23 from each parent), which would result in what is referred to as a chromosomal defect.
We use words to count with as well as numbers, and some count words or use words to count numbers, but do not typically apply counting behavior to the ideas being expressed in Mathematics. For example, whereas we note that Yin and Yang is a pattern-of-two (or duality, dichotomy, complementarity, etc...) and may well make a list of the numerous pattern-of-two examples that some may quantify overall; it is untypical to find someone applying counting behavior to mathematics itself. For example, when we note the duality of add/subtract and/or multiply/divide, we do not regularly find people referring to such ideas as patterns-of-two. Nor do we find it a typical idea for someone to make a list of three-patterned ideas found in mathematics such as Sine- Cosine- Tangent, A2 + B2 = C2, or Mononomial- binominal- polynomial (1- 2- Many), nor refer to a quadratic as a doubled pattern-of-two. Whereas we use a rudimentary form of mathematics to count persons, places and things, it is not typical to find an ongoing research project in which mathematics itself is being scrutinized to uncover its own mathematical patterns which define a type of limited and limiting cognitive behavior being engaged in.
Whereas we are taught to use mathematics to count with in very elaborate ways called equations with which to analyze, you do not routinely find, even at the highest levels of education; those who teach a method by which mathematics itself can be analyzed for its repeating numerical patterns which define a type of cognitive behavior being exercised. To do so brings us to the realization that many of the ideas being expressed in Mathematics are being used elsewhere, such as the already recognized presence of mathematics in music, gaming (gambling), and baking... to give but three examples. If someone were to tell you that language can be used to quantify the ideas found in mathematics and that by doing so it will be found that such patterns are found in other subjects, you may or may not agree... nor further consider that such a listing of patterns exhibits an ongoing display of a cognitive limitation. Though some might want to dispute this by claiming there are multiple types of thinking, the underlying patterns of all types of thought processing exhibits the same patterns and those patterns are limited. It is much like putting together a list of all basic elements only to find the list is actually quite small, but rationalize this recognition away through a process of practiced minimization by way of focusing on the presumed importance of a given element due to its multiplicity of usage in our day to day lives. Rationalization, Repetition, and Embellishment are recurring themes in mathematics, as well as all subjects.
With respect to patterns-of-two, it is untypical to find someone considering that the repetition of a bi-pedal gait may have been instrumental (on some level), in establishing a routinization for thinking in terms of opposite, dualities, dichotomies, pairs, etc... And yet if we look for environmental or physical events of repetition which could be used to influence other patterns such as the triplet code in DNA, we are met with obstacles. Such is the case for all quantifications... we are met with obstacles to the extent we can come to realize that if DNA is part of Evolution, why is it so stubbornly set in its way of maintaining a triplet code instead of evolving towards a four, five, six, seven, eight, nine, etc., code? Similarly, why aren't there 300 million elements and not just simply 118 Chemical Elements? Similarly, why is there a recurring "three" quantity amongst Nuclear particles and not millions?

Three progressively heavier copies of each type of matter particle exist, and no one knows why. A new paper by Steven Weinberg takes a stab at explaining the pattern.
Three particles labeled "e" for electron, "mu" for muon, and "tau" for tau particle line up horizontally, with successively bigger auras around them signifying larger mass. Puzzlingly, the laws of nature appear to be composed in triplicate, with three copies of all matter particles, each heavier than the last but otherwise identical. The universe has cooked up all sorts of bizarre and beautiful forms of matter, from blazing stars to purring cats, out of just three basic ingredients. Electrons and two types of quarks, dubbed "up" and "down," mix in various ways to produce every atom in existence.
But puzzlingly, this family of matter particles – the up quark, down quark and electron – is not the only one. Physicists have discovered that they make up the first of three successive "generations" of particles, each heavier than the last. The second- and third-generation particles transform into their lighter counterparts too quickly to form exotic cats, but they otherwise behave identically. It's as if the laws of nature were composed in triplicate. "We don’t know why," said Heather Logan, a particle physicist at Carleton University. (Why Do Matter Particles Come in Threes? A Physics Titan Weighs In. by Charlie Wood, March 30, 2020)
Atomic particles are being counted. Elements are being counted, change in one's pocket is counted, the days of a month are counted, and many other items are likewise being counted... but the usage of numbers by way of Mathematics is not typically being subjected to a count. You may use words such as triplet, pair, binomial, quintuplet, etc., but the usage thereof is not being counted as an expressed limitation of cognitive behavior. We do not teach nor exercise an activity involving the subjection of Mathematical ideas to a count and then comparing this tabulation to all other ideas which customarily have not also been similarly subjected to a count. In so doing, we will uncover that the human mind is practicing a limitation and that the reason for this limitation is that we humans, as a biological organism, are required to establish some measure of equilibrium in the confines of the environment to which we find ourselves in. The one which we are involved with is incrementally deteriorating, and this calls for the usage of limitations in order to adopt some semblance of survival in conditions whose resources are dwindling.
By subjecting the subject of Mathematics to the same rigor of counting we use in other subjects, we can identify the presence of a limitation in the thought processing of humans. When you come to realize that there are numerous patterns-of-two in mathematics and this is being used to determine the three- patterned world of atomic particles, something appears to be out-of-sync with our thinking. It is much like the usage of a military service that functions as a type of Communal Socialism as a means to protect a so-called Democratic society. If a Democracy is superior to Socialism and Communism, then it is a stark hypocrisy to use a Military that is not a functional Democracy, to protect it. When we claim that a hallmark of a Democracy is the ability to vote in one's leaders and find that enlisted personnel do not vote in their leaders, the realization that Military service is not a Democracy is a slap in the face to logic. Similarly, in a so-called Democratic society we find multiple Institutional activities that express a type of autocratic or dictatorial blueprint such as being told what to do by a boss, a film director, a coach, or educational instructor. We have a democracy in order to freely exercise multiple forms of a non-democratic exercise and not be even aware that we are doing so? Are we particularly stupid or what?

Current Mathematics is like many individuals who do not want to be tracked, observed or have their lives unduly scrutinized for fear of being manipulated. Mathematicians do not want their subject subjected to a form of analysis which may very well indicate that their activity is an exercise commonly used by others in their own way, in their own interests such as when playing chess or doodling. Mathematicians want their subject to be the Queen of all forms of logical thinking, as well as being able to map out all types of thinking, be it creative, original, illusory, bizarre, psychotic, philosophical, poetic, supernatural, religious, science fiction, mechanical or whatever. To suggest that the so-called language of mathematics can not only be analyzed like the parts of a sentence but as a common theme of patterns to be found in multiple subjects which can thus render its self-image to a level of commonality not conducive to its egotistically defined importance, is much like taking away the self-proclaimed and established entitlements which Journalists have frequently tried to flaunt in any and all situations felt to be their provenance of ownership.
Whereas some claim that mathematics exists in all things, they do not also claim that there are things in mathematics which are not accurately being accounted for nor defined in the context of exhibiting underlying patterns which reflect a commonality of thought processing which details the current state of affairs related to humanity and the incrementally deteriorating environment. (I am referring to the slowing of the Earth's rotation, the decrease in the Sun's energy, and the receding of the Moon.)
Typically, when it is mentioned that someone wants to analyze mathematics in terms of the ideas being expressed, it is thought that one is referring to the analysis of how someone is using mathematics for a given task. For example:
The frame analysis method consists of multiple steps to observe, describe, interpret, and analyze students' mathematical thinking processes when they are solving mathematics problems. (Analyzing Students' Mathematical Thinking in Technology-Supported Environments by Zekeriya Karadag, 2009)
This is not what I am speaking of in this present context. I am talking about the analysis of Mathematical ideas exhibiting patterns which are quantifiable. We will find that there is an abundance of two-patterned ideas, with lesser amounts of other ideas and an overall limitation being expressed. The fact that we can find limitations not only in mathematics but all subjects presents us with the realization that the presumed limitlessness of human imagination and overall thinking is a lie. Most day to day activity apparently reflects routinized repetitions, including those presumed to be original ideas. Whereas individuals can express activities or ideas that can be labeled as creative, such creativity may well be frequently expressed in different contexts throughout the world... but we do not today have a means to catalog all behavior occurring everywhere all the time in order to pay witness to which behavior is truly creative or original in the sense of having never occurred before in any context by anyone. The same original idea may occur to multiple people, yet none of them are in a position nor have a means of recording the originality, whereby someone else at some other place and time may receive credit for the same idea or activity due to circumstances of visibility and recording. Many people have unique ideas that are later found to be used by someone else that is making money off of the same or similar idea which was not originally put into practice by the actual originator who simply comes to express themselves or others that they too had a particular idea much earlier than those who are using it (typically) for a financial gain or a means by which one or more others can be manipulated by the commentary thereof to those who will interpret the display of such as a uniqueness to defer to.
The so-called (symbolic) "Language" of Mathematics is typically preceded by the conventional language in which words are displayed. That is unless upon when looking at the precursors of language such as infant Babbling, we decide to interpret the vocalizations of infants in the dimension of mathematics and refer to it as counting. That is... if we count the quantity of utterances as well as the quantity of quality in babbling; where some researchers of infant vocalization behavior may generalize the content as being a variety of sounds, yet fail to note that there is a limited variety of sounds... and that the word "variety" can be viewed in the context of representing a quantity... though the quantity may differ from person to person, just as the word "many" or the phrase "a few" may represent different quantities from person to person if they were asked. In other words does "a few" mean two or three or four, or more than five but less than ten? Does "many" mean also a variety and both of them represent a set limit?
If we run a query at Related words such as for the word "amount" to find words describing what the parameters of the program defines as relatedness, we should take into consideration the limitations of the tool:
Related Words runs on several different algorithms which compete to get their results higher in the list. One such algorithm uses word embedding to convert words into many dimensional vectors which represent their meanings. The vectors of the words in your query are compared to a huge database of pre-computed vectors to find similar words. Another algorithm crawls through Concept Net to find words which have some meaningful relationship with your query. These algorithms, and several more, are what allows Related Words to give you... related words – rather than just direct synonyms.
As well as finding words related to other words, you can enter phrases and it should give you related words and phrases, so long as the phrase/sentence you entered isn't too long. You will probably get some weird results every now and then - that's just the nature of the engine in its current state. Special thanks to the contributors of the open-source code that was used to bring you this list of amount themed words: @Planeshifter, @HubSpot, Concept Net, WordNet, and @mongodb.
When we note that letters of the alphabet are divided into Consonants and Vowels, do we also find this kind of two-part divisioning in basic Mathematical concepts such as addition and subtraction? When we find that we place a comma after every third number in terms of placement (1,000,000,000), is this similar to t the separation of 3 or four items in a sentence? Do both exhibit a similar cognitive profile being used in different contexts? And when we find that a list of four amino acids in DNA and RNA can also be separated by a 3 to 1 idea, can we thus infer something very basic is taking place but no one is making the connection because they do not know how to count basic cognitive activity expressed in our symbolisms from different subjects?
Here is a link to multiple three-to-one ideas which reflect the comma used in mathematics to separate a group of three from a singularity: Three-To-One ratios Page A
| Item | --- Three the same --- | --- One is different --- |
| DNA = | Adenosine- Cytosine- Guanine | Thymine |
| RNA = | Adenosine- Cytosine- Guanine | Uracil |
| Item | --- Three are similar --- | --- One is different --- |
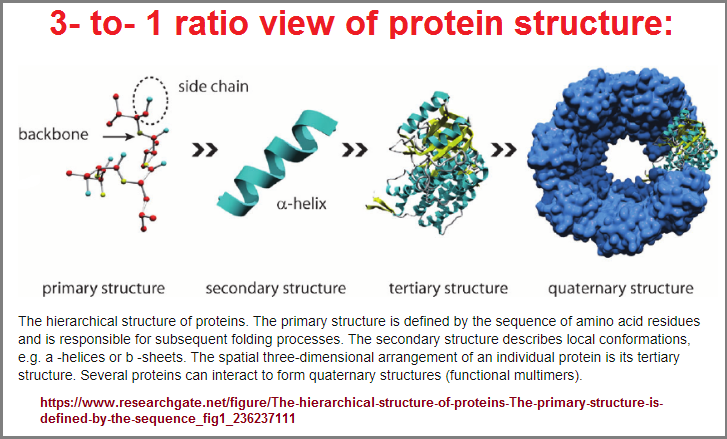
| Protein structure = (such as in the ribbon model) |
Secondary (2)- Tertiary (3)- Quaternary (4) | Primary |
What is Babbling? by Katie, Oct. 10th, 2001 Babbling is referred to as a pre-linguistic skill: meaning a skill that happens prior to the development of language and speech.
There are Three Types of Babbling
- Marginal Babbling: This babbling usually happens between 4-6 months of age. You will hear your infant put together consonant-vowel (CV) or vowel-consonant (VC) sound combinations, like "baaaa”, "maaaa”, or "uuuum.” Marginal Babbling is considered a type of Pre-canonical Vocalization along with squeels and cooing.(Sidenote: Before this phase, between 1-4 months, your infant should be cooing. Cooing refers to your infant producing sounds that are vowel like i.e. oooooo and aaaahhhhhh. Often times infants will produce these coo's when having face-to-face interactions with a care-giver).
In the time period between six and ten months of age, your infant will begin to use more of a variety of sounds and sound combinations referred to as canonical babbling. Canonical babbling is divided into two subtypes: Reduplicated and Non-reduplicated.
- Reduplicated Babbling: This refers to when your infant repeats the same syllable over and over, such as "babababa” or "mamamama” or "gagagagaga”.
- Non-reduplicated Babbling: In this final stage of babbling, your infant’s sounds are now more varied. Rather than producing the same syllable over and over, he will now start to combine different sounds and syllables like "bama” or "gagameee”.
After the three types of babbling, we come across a one-word, two-word, three-word stage of vocalization followed by a multiplicity of combinations which can be expressed mathematically as a reference to the three-items separated by a "developmental comma" followed by another sequencing of three. (Speech development by Graham Williamson, 11 Jan. 2014) A "developmental comma" can be alternatively described as a conjunction, developmental shift, maturational stage, or even pause, idle, conjunction, or yellow light. The same thing occurred in the development of a number concept by primitive peoples that may be referred to as cognitive stops and starts or milestones. With respect to amino acids, let us reference the existence of 3 stop codons and 1 start codon.
Interestingly, in a attempt to answer why 3 stop and 1 start codons (a 3-to-1 ratio), these researchers use a two-patterned binomial theorem:
Abstract
We examine the standard genetic code with three stop codons. Assuming that the synchronization period of length 3 in DNA or RNA is violated during the transcription or translation processes, the probability of reading a frame-shifted stop codon is higher than if the code would have only one stop codon. Consequently, the synthesis of RNA or proteins will soon terminate. In this way, cells do not produce undesirable proteins and essentially save energy. This hypothesis is tested on the AT-rich Drosophila genome, where the detection of frame-shifted stop codons is even higher than the theoretical value. Using the binomial theorem, we establish the probability of reading a frame-shifted stop codon within n steps. Since the genetic code is largely redundant, there is still space for some hidden secondary functions of this code. In particular, because stop codons do not contain cytosine, random C → U and C → T mutations in the third position of codons increase the number of hidden frame-shifted stops and simultaneously the same amino acids are coded. This evolutionary advantage is demonstrated on the genomes of several simple species, e.g. Escherichia coli. (Copyright © 2012 Elsevier Ltd. All rights reserved.
(Why has nature invented three stop codons of DNA and only one start codon? by Michal Krí&zuml;ek and Pavel Krí&zuml;ek)
In an effort to understand why there is a 3 to 1 (ratio) occurring in codons, it is necessary to take into account the ratio's presence in other subjects in an effort to pay witness to a pattern that is not seclusively limited to one topic in one subject area. For example: Three-To-One ratios Page A and 3:1 Ratio Biology as Poetry by Stephen T. Abedon, Ph.D..
If we note a set variety as being the sounds described with two-letters (found in babbling) such as Ba, Bi, Da, Di, Na, etc., we might further describe the utterances over-time in a sequence which displays single, then double, then triple sound groupings, with long strings (or "many") utterances occurring prior to a display of sounds we might interpret to be words. For example:
- Ba
- Ba-Ba
- Ba-Ba-Ba
Clearly we can recognize a 1, 2, 3 sequence, though the idea of an infant unconsciously engaging in a rudimentary form of counting behavior may not come to one's mind. Like wise when we observe a child's first attempts at uttering what many have termed to be a child's "first word". Yet, a second and third word may otherwise be taken for granted, whereby no further attempts to quantify the usage of words may be engaged in. For example, a child may utter the word "Up", that is eventually followed by two-word groupings by way of repetition, thus expressing a similarity of cognitive behavior seen in the duplication and reduplication of a single word such as "Up- Up".
The point to be made is that we are confronted by linguistic behavior that we do not typically defined as a type of rudimentary counting scheme, though once we learn to pay attention to the quantity of words and speech patterns, we can clearly make note of repetitions which can convey the idea of a primitive person's attempts to practice a simple system of cardinality.... such as 1, 2, 3... and the lack of a speech pattern that can be viewed as an expression of "zero". In other words, whether or not there is a conscious appreciation of a person making the observation that their speech patterns exhibit a type of seriality which may or may not exhibit cardinality and may otherwise exhibit counting by twos, or threes, or some mix and match pattern like a Fibonacci Sequence; the question to be asked is whether such vocal behavior constitutes an underlying usage of numbering, like that being described in some animals. In one instance, we find the test for an animal's ability to count referenced by an embellished two-patterned criteria expressed in a three-patterned way:
Animals need to exhibit behavior which humans can interpret to mean the animal can distinguish the following:
- How many?
- Is there more than...?
- Is there less than...?
Test for counting are similar to tests for color vision, in that they usually involve a two-step process, first giving the test animal the opportunity to learn (count) objects, and then giving the test animal a choice between sets, one of which has the same number of objects as the learned set. Source: Animal Counting Behavior
Abstract
A definition of counting is adopted from R. Gelman and R. M. Gallistel (1978) and Piaget (1952) that allows for a comparison between animal and human counting behavior. The evidence, which ranges from early anecdotal reports to modern experimental analyses, suggests that a variety of infra-humans ranging from birds to primates can learn to count, although successful demonstrations are most likely to occur under relatively extreme experimental conditions when alternative predictors of food or safety are unavailable. Counting behavior appears to be a relatively unnatural response in infra-humans, and its acquisition may reflect the boundaries of the animal's associative abilities. (84 ref) (PsycINFO Database Record (c) 2012 APA, all rights reserved)
Counting behavior in animals: A critical evaluation by Hank Davis and John Memmott; November 1982, Psychological Bulletin 92(3):547-571, DOI:10.1037/0033-2909.92.3.547
In conducting experiments, we frequently see the usage of patterns-of-two and/or three, which may include the quantity of researchers involved in a give research project. In other words, the collaboration being used may itself signify an unrecognized act of counting behavior on the part of the experimenters themselves... if not also in the quantity of subjects but the quantity of trials, or the duration, etc.., such as a three-year, or three-month or three-week study interval, or every other third event, participant or some other criteria that can itself being quantified but remain oblivious from the researchers themselves and other researchers who review their work and likewise use some countable exercise in their own efforts to achieve what they may consider to be a critical or comprehensive analysis of "all" available data, but do not actually provide a number as to what they mean by "all".
If infant babbling behavior is an unrecognized practice of numerousity, like the supposed unconscious or defined as "instinctual" behavior of animals that appear to have some 'sense' of rudimentary counting behavior, can we also say this is the case for the sounds emitted by insects... or all sounds, regardless of origin? If we quantify the electro-magnetic spectrum and quantify the number of basic elements, are such valuations also an appreciation of a universal language of expression to be defined as math... that is, counting... or is this little more than an imposition we humans are placing onto different perceptions in an effort to establish a pattern... for whatever reason, if "reason" is the correct choice of labeling?
With respect to word sounds described as language, we further note that those who are deaf tend to have difficulty in articulating words which are needed for conventional mathematics. While one may argue that a deaf person such as Beethoven can produce works of musical art, but deafness acquired later, that is, after one has already learned how to use common verbal language is different from someone whose first language is American Sign Language (ASL) (because of being born deaf). In short, a grasp of language usage involving words is an important requirement for pursuing the language expressions of mathematical equations. This is not to say that deaf students are unintelligent, it is to say that their brains use a different type of symbolic mental processing; much of which is context (culturally) dependent.
What is known about deaf children and mathematics learning?
Overall, the point I want to make is that there is a dimension of language that is being overlooked with respect to mathematics and hearing. It is a rather curious think to note that many operations in mathematics involves the usage of dichotomies (Dualities and Simplistics in Mathematics page 1), like an infant babbling in patterns-of-two, or a primitive person having stopped in the development of their counting scheme; while the presence of fewer patterns-of-three suggests that at least some thinkers have developed a means by which to conceptualize beyond the "two" (and its doubles such as quadratics), to achieve a recognizable usage of a 'three' quantity.
Mathematics language expresses cognitive indices of quantity which often go unrecognized, just as an animal such as a dog is (assumedly) oblivious to the quantity of barks it makes in a given utterance, or the types of quantifiable barks being made. No less, do crows recognize their usage of caws as a number, or is it only we humans who describe a cawing behavior as exhibiting three, or two, or four, or one caws? Similarly, does a person knocking on a door recognize how many times they customarily knock in a given situation for a given purpose, or are they engaging in knocking in an unconscious expression that can be quantified and thus interpreted to reflect an underlying cognitive behavior? Does counting reflect an obsessive compulsion to complete an activity a certain number of times, or do many of us count... such as how many times a person coughs, or sneezes, or use the restroom, or eating a volume of food, etc., yet never tell anyone because they interpret such a recognition as being weird... in the sense of too uncommon and therefore strange and illustrative of something that is not considered to be normal?
Many people (apparently) are conscious counters. If not our own behavior than that of one or more others. We may count calories, sets in weight lifting, duration and/or distance of a walk, hike, bike ride or jogging event. We may count how many fish we catch or bullets shot from a rifle. However, if such counting behavior is not routinized by others into a frequency of attendance by multiple others (such as counting how many A's one gets in school), then counting behavior that is atypical, may be viewed as something that is non-normal. If the person is highly suggestible, one or more influential others can use the situation to distort the person's view of reality by describing the situation as an indication of a medical or mental condition that needs treatment, whereby the scenario becomes a useful tool by which someone can engage in an ulterior motive that is not beneficial to the person engaged in the atypical counting behavior.
Mathematics can be quantified, though it is typically used as a quantifier. When you observe such expressions as plus/minus, add/subtract or 1,2,3..., you are paying witness to quantities that can be described as patterns-of-two, patterns-of-three, dualities, binomials, trinomials, etc... The reason for doing so is to establish the existence of a recurring cognitive theme which occurs in different subjects with their own symbols. However, again we eventually return to the comparison of hearing to speech. Yet a problem exists in that the different schools of linguistics as well as audiology are overlooking the need for establishing the accountability of counting in their respective interests and then correlating the numbers being found. If we find there is an over-riding usage of two-patterned ideas being used in mathematics, yet language and hearing rely on a more dominant usage of three-patterned references, one might easily conclude that present mathematics is in a backward state of development, if development, under most circumstances, follows nor only the Cardinality of a 1,2,3 profile of quantification, but also a specific order (Ordinality), if not simply as a generality such as in the Nominal (naming) case of identification.
In the example of the idea of a simple mathematical operations sequence in which letters are used as a mnemonic (PEMDAS: please excuse my dear aunt sally) to reference "parenthesis, exponent, multiplication, division, addition, subtraction", we see both quantity and order as well as nominality. The same thing occurs in grammar and developmental biology. For example, it is not uncommon to find a person referring to a Noun as a person, place, or thing... which provides us with a three-part definition occurring in a given sequence involving names. It is not too difficult to see an underlying mathematical activity even though most people do not attribute quantity, order and naming as a reference thereof. Words, Ideas, behaviors, events, etc., all occur in a given order, though the order may reflect the different positions we seen in linguistic typology (such as the arrangement of Subject- Object- Verb ) found in Language Classification>.
There are two kinds of classification of languages practiced in linguistics: genetic (or genealogical) and typological. The purpose of genetic classification is to group languages into families according to their degree of diachronic relatedness. For example, within the Indo-European family, such subfamilies as Germanic or Celtic are recognized; these subfamilies comprise German, English, Dutch, Swedish, Norwegian, Danish, and others, on the one hand, and Irish, Welsh, Breton, and others, on the other. So far, most of the languages of the world have been grouped only tentatively into families, and many of the classificatory schemes that have been proposed will no doubt be radically revised as further progress is made.
A typological classification groups languages into types according to their structural characteristics. The most famous typological classification is probably that of (1) isolating, (2) agglutinating, and (3) inflecting (or fusional) languages, which was frequently invoked in the 19th century in support of an evolutionary theory of language development. Roughly speaking, an isolating language is one in which all the words are morphologically un-analyzable (i.e., in which each word is composed of a single morph); Chinese and, even more strikingly, Vietnamese are highly isolating. An agglutinating language (e.g., Turkish) is one in which the word forms can be segmented into morphs, each of which represents a single grammatical category. An inflecting language is one in which there is no one-to-one correspondence between particular word segments and particular grammatical categories. The older Indo-European languages tend to be inflecting in this sense. For example, the Latin suffix –is represents the combination of categories "singular" and "genitive" in the word form hominis "of the man," but one part of the suffix cannot be assigned to "singular" and another to "genitive," and –is only one of many suffixes that in different classes (or declensions) of words represent the combination of "singular" and "genitive."
Note: "genetive" can be quantified as "multiplicity", thus giving rise to "1 and many" from the words "singular and genetive"; which also is seen in the US monetary expression of E pluribus unum (out of many, one). Both of which are expressions of a cognitive numerousity. While using quantity may be described as an example of the Cognitive dimensions of notations, it is not customarily listed. Whereas we do see a reference for The Magical Number Seven, Plus or Minus Two by George A. Miller, we do not also see a reference to the underlying three part ensemble of 5-7-9. Instead, the "7" and "2" are emphasized in the title and are used as a reference of some significance by those who are interested in the number 7 and/or 2.
While identifying an underlying cognitive dimension in mathematics ideas with respect to using the tool of quantification is of value, the usage of quantification may well have its own underlying cognitive substrate which is, in a sense, a 'bare bones" appraisal of recurring cognitive patterns related to biology constrained by the incremental deteriorations of the Earth's rotation rate, the Moon's receding, and the Sun's energy burnout.
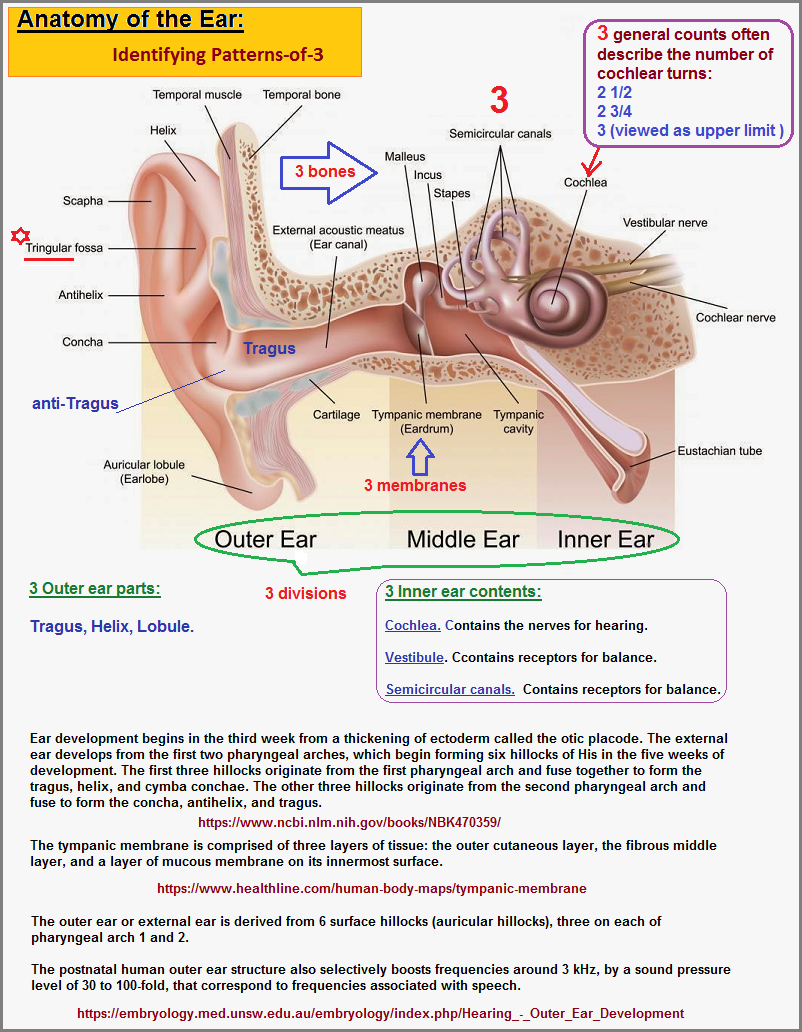
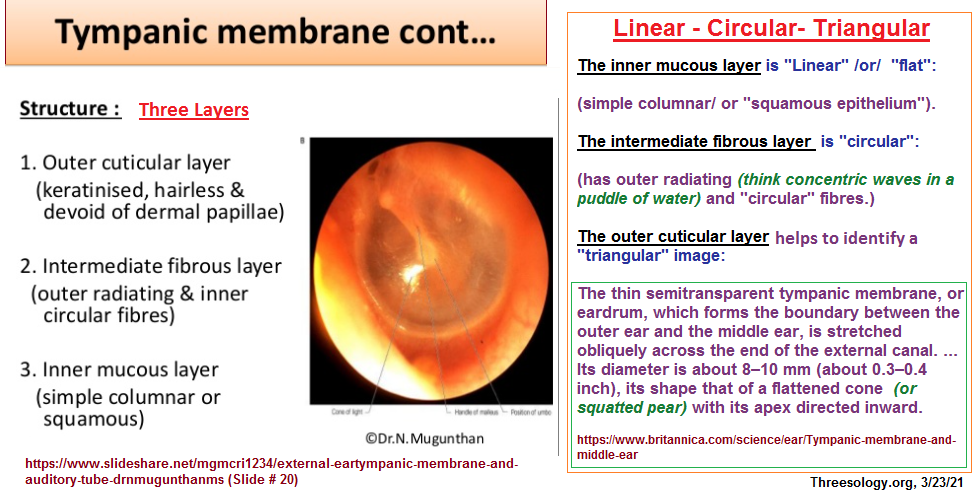
The language of mathematics must be viewed in the context of other verbally influenced behavior which brings us back to a consideration of what role the processes of hearing play a role. No doubt that a recurring (numerically identifiable) theme (as well as an absence thereof) has some value, such an examination is not typically considered in different perspectives involving ideas (philosophy, linguistics, etc...). It is not common to find anyone speaking to the recurrence of a numerically identifiable pattern. While mathematicians can routinely use numbers to make abstract correlations, to do so without making an associative claim that one is engaged in a type of mathematically-based analysis is thus interpreted in a negative sense, such as someone who is engaged in valueless correlations such as numerology. The fact that only a few (numerically identifiable) patterns can be found is significant. Let me point out a recurrence in the structural components of the ear involving patterns-of-three. To have some other-than-three dominant pattern might well result in a different type of hearing and speaking ability, and thus mathematical orientation as well. The fact that mathematics relies heavily on patterns-of-two ideas suggests there is some as yet unrecognized processing influence taking place, just as was the usage of patterns-of-two in the Yin/Yang ideas of duality and complementarity.
Further references: Language threes page 1
Page Origination: May 27th, 2021...2:02 AM
Initial Posting: May 28th, 2021...7:55 AM
Updated Posting: July 17th, 2021... 9:12 AM