(Static -vrs- Dynamic Equations)
10
~ The Study of Threes ~
http://threesology.org
Visitors as of 2/27/2021


Instead of using a bullet list format I chose to use an enumerated one to make a point about all lists being conjured up by us humans:
that is: –repetitively espoused constraints...
—exhibiting an overlooked pattern that is subject-wide.
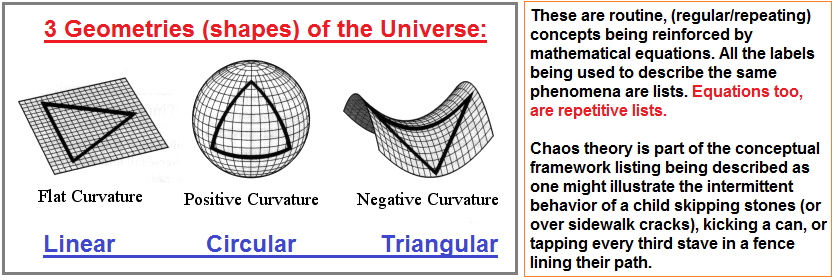
The three theories concerning the shape of the Universe, alternatively described as The 3 geometries of the Universe:
- flat (or linear)
- positive curvature (or spherical/circular
- negative curvature (or saddle-shaped/triangular)
These three items represent a list of regularity in the conceptual framework of humans. In other words, whether we cite a 3-patterned recurring usage of ensembles, or groupings or sets such as:
- Linear- Circular- Triangular: (Linear, Circular, Triangular configurations page 1)
- zero- one- two
- one- two- many (Generalized representation of sequencing found in early counting systems.)
- Triple anatomical configurations: (List of Three's in Anatomy by Dr. McNulty and associates)
- 2- 3- 4
- 4,5,6
- 7...8...9
- 10, 100, 1000
- xyz
- 3 researcers, 3 subjects, 3 month study
- abc
- up-down-in between
- Lights, Camera, Action
- 3 generations of particles
- Horizontal, Vertical, Diagonal (Typical directions for moving playing pieces on board games such as checkers and chess.)
- minimize-maximize-close (Rule-of-thumb used in the upper right hand corner of computer screens.)
- yin-unity-yang, etc.,
- Negative oppression- "Equilibriated" oppression- Positive oppression (Types of oppression being used by governments.)
We can also place a list of two-patterned configurations or some other enumerated sequencing which may occur over larger areas and wide-spread times making the connections of inter-activity more difficult to discern and correlate as continuities... they all represent an underlying structural component to our ideas developed by a brain processing activity subjected to an incrementally deteriorating environment which enforces compliance as a survival mechanism, which leads us into the behavior of adopting rationalization as a tool for maintaining some semblance of equilibrium in a chaotic system. "Chaos" in this sense being defined as a system of changes which we navigate haphazardly with.
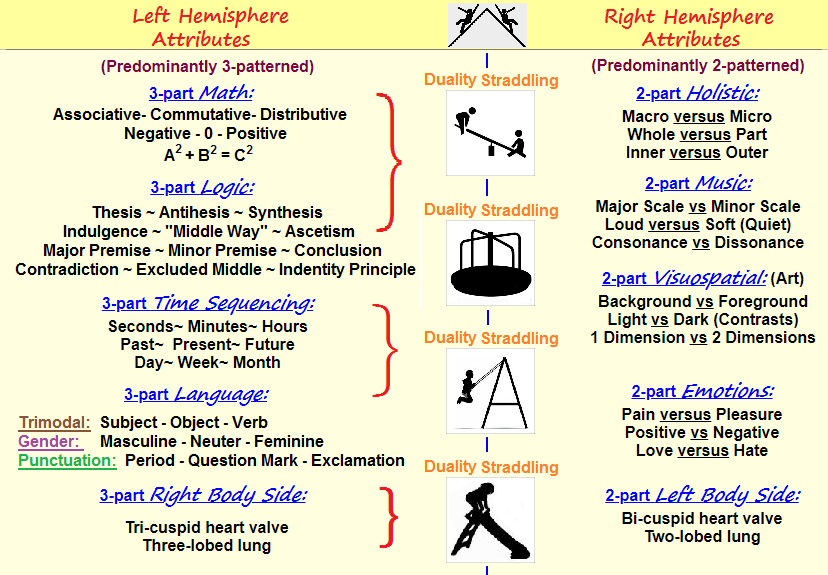
The "three" model, and the "two" model as well as the few other recurring models being used by human conceptual processes (despite the elaborations used within the boundaries of the employed language and symbolism of different subjects); the design(s) is/are expressing a recurring theme of patterned conceptualization that we can and do elaborate with different signs, symbols, numbers, words or attributes such as art, music, poetry, experimentation, technology, etc..., but the underlying usage of given patterns remains the same or similar... like the genetic code or three-patterned arrangement of atomic particles (protons- neutrons- electrons) apparently remains the same. Because genetics is part of evolution, one would think that it would more consistently provide evidence of being governed by the assumed "law" of evolution, but we are otherwise confronted by an extremely persistent conservation in that the triplet code has been sustained and not evolved beyond a triplet code, unless that such a code requires a longer period of time or other-than-typical environmental factors to begin changing. However, we cannot permit this consideration to be used as a definitive explanation which keeps us from thinking otherwise.
Chaos theory is part of the conceptual framework listing, and is therefore not a random phenomena of thought (even if your friends, colleagues, siblings or significant others appear to be chaotic in their thinking at times), though interpretations generally try to describe behavior which may appear random... and then fail to report the cyclicity of the randomness itself. However, some researchers come to identify regularity in randomness which may be time, distance... along with mass and speed dependent... which the slowness which humans create equations does not typically provision them with the idea of taking this measure into consideration as a variable. Interdependency is a regularity despite occasional interpretations which selectively identify what may viewed as peculiarities that are eventually described mathematically and provide the developer with an idea for which they receive some award for... for not over-turning the apple cart of accepted rationales too far or else be labeled a "fringe" researcher dabbling too far afield with unsubstantiated correlations and suppositions.
Mathematics applied to physics problems are like people inclined to use their own language that they are most familiar with, in that it adds to the mystique of concepts as if a foreign language not only provides privacy but an exclusionary principal like a secret handshake. password, moniker, dress code, Identity card, etc., for particular club members participating in an exercise of exoticism as did many sects in ancient history. Nonetheless, once a person wades through the morass of language peculiarities used as ritualisms of thought and mathematical (symbolic) expression, we find repetitions and limitations in the currency of thought being employed. For example, from this paper: Strange Attractors and their periodic repetition by Quodong Wang and Ali Oksasogulu, we find this Abstract:
In this paper, we present some important findings regarding a comprehensive characterization of dynamical behavior in the vicinity of two periodically perturbed homoclinic solutions. Using the Duffing system, we illustrate that the overall dynamical behavior of the system, including strange attractors, is organized in the form of an asymptotic invariant pattern as the magnitude of the applied periodic forcing approaches zero. Moreover, this invariant pattern repeats itself with a multiplicative period with respect to the magnitude of the forcing. This multiplicative period is an explicitly known function of the system parameters. The findings from the numerical experiments are shown to be in great agreement with the theoretical expectations. VC 2011 American Institute of Physics. [doi:10.1063/1.3567009]
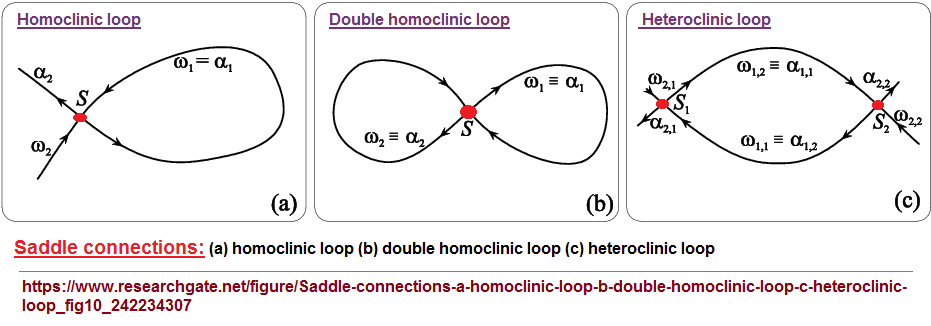
- Homoclinic: (mathematics) Describing a path that starts and ends at the same point of equilibrium. ( Homoclinic Meaning)
- Heteroclinic: (mathematics) Describing a path between two points of equilibrium. (Heteroclinic meaning)
- The Duffing equation (or Duffing oscillator), named after Georg Duffing (1861–1944), is a non-linear second-order differential equation used to model certain damped and driven oscillators. (Wikipedia: Duffing Equation)
- Manifold, in mathematics, a generalization and abstraction of the notion of a curved surface; a manifold is a topological space that is modeled closely on
Euclidean space locally but may vary widely in global properties. Each manifold is equipped with a family of local coordinate systems that are related to each
other by coordinate transformations belonging to a specified class. Manifolds occur in algebraic and differential geometry, differential equations, classical
dynamics, and relativity. They are studied for their global properties by the methods of analysis and algebraic topology, and they form natural domains for the
global analysis of differential equations, particularly equations that arise in the calculus of variations. In mechanics they arise as "phase spaces"; in
relativity, as models for the physical universe; and in string theory, as one- or two-dimensional membranes and higher-dimensional "branes."
(Britannica: Manifold)
- Brane: In string theory and related theories such as super-gravity theories, a brane is a physical object that generalizes the notion of a point particle to higher dimensions. Branes are dynamical objects which can propagate through space-time according to the rules of quantum mechanics. They have mass and can have other attributes such as charge. Mathematically, branes can be represented within categories, and are studied in pure mathematics for insight into homological mirror symmetry and non-commutative geometry. (Wikipedia: Brane)
- Brane: an object extended in one or more spatial dimensions, which arises in string theory and other proposed unified theories of quantum mechanics and general relativity. A 0-brane is a zero-dimensional object, a point; a 1-brane is a one-dimensional object, a string; a 2-brane is a two-dimensional object, a membrane; and a p-brane is a p-dimensional object. Because some versions of string theory have 9 spatial dimensions, p-branes may exist for values of p up to 9. (Britannica: Brane)
- Entomologically, the word "Brane" comes from "membrane".
- 3 branes page 1
The use of "brane" in physics by way of mathematical computations yields the same underlying considerations we find when some scientists describe a cell membrane as a "Bi-lipid" layering, and a previous interpretation involving the idea of a sandwich called a trilaminar construction. It all depends on how you want to look at the layering and whether you prefer a "two-patterned" orientation or a three-patterned one. (The Devil's Advocate and 3's Research, page 9)

 |
Roman dicers from a fresco at Pompeii, playing what is thought to be an early version of backgammon. The cartoon-like captions above their heads describe a disputed call: the man on the left cries, "I've won!" while the one on the right objects, claiming, "It's not a three, it's a two." Analogously, the two characters can be viewed as the right & left hemispheres of the brain. The right adamantly refuses to acknowledge the left's
claim to a 3 and insists that the "3" the left sees is actually a 2. If the overall purpose of the "game" (life) is to achieve a "3" and yet there is a
claim from some for a preponderance of "2" (with all its various guises), do we try to change the rules of the "game" or create a teaching methodology
which enables the distinctions of "2" and "3" to be made identifiable and useful from all vantage points? (Even if the purpose of the game is defined by
Earth-specific environmental circumstances.) The social problems created by an underlying 2 versus 3 contention has been going on for long enough... since
Pompeii anyway. Let's not leave a similar picture of us for future historians who find it beneath the rubble of an extinct civilization. |

Threesology Research Journal (Home page)
Similarly, we find this taking place in theoretical physics as well, with mathematics top-heavy in its leanings towards the usage of dichotomies such as found in add/subtract, multiply/divide and multiple other examples found here: Dualities and Simplistics in Mathematics page 1.
While this wikipedia link gives some general understanding of Homoclinic orbits, this link may be more profitable for some readers: Homoclinic points and resonance in dynamical systems by Kasperczuk, S. & Gaska, S.. While I am not directed towards a discussion of the topics as they are outlined, I wanted to supply some "real-world" examples of conceptualizations regarding theoretical approaches of geometrical approaches at grappling with an attempt to grasp assumed dynamical systems exhibiting repetition, fluctuations, and periodicities that some observers may not be able to readily appreciate as an illustration of static versus dynamic perceptions involving the same idea being expressed mathematically. Such items serve to illustrate cognitive lists... or listings which describe limitations. An instability in a manifold must manifest itself as a regularity or we won't be able to recognize it with a static labeled such as equilibrium or disequilibrium. The presence of dichotomous thinking is evident. Regularly thinking about irregularity of occurrence creates stability which can influence the coloring of that being observed. In other words, if we stabilize an instability with our language and equations, we have created a list that may delude us to view a static system as a dynamic one and vice-versa. Standard Cognitive patterns are recurrences which influence us to cater our minds towards "safe zones" which utilize the same underlying patterns albeit perhaps with different labels consistent with a given subject. Standard Cognitive Models present us with Homo- and Hetero-clinic loops which we can alternatively describe as variations of the old yin and yang separations, complimentarities, and contrasts. It is like a binary computer code to which we apply a three-patterned boolean logic. Even when an equation is labeled as being non-linear, they are nonetheless linear in form and functionality.
The idea of Chaos Theory is a good example of static and dynamic systems, except that when looking at /Chaos from a different vantage point, three... and not just two properties of chaotic systems have been recognized:
- Sensitive dependence: the tendency for complex, dynamic systems to be highly sensitive to initial conditions, so that two such systems with starting points that are almost identical may become extremely divergent over time. In other words, the future states of complex systems are very dependent on small differences in their initial states. The best known example of sensitive dependence is the so-called butterfly effect. One possible explanation for this phenomenon is that measurements in chaotic systems are imprecise, so that prediction becomes extremely difficult.
- Deterministic System: In mathematics, computer science and physics, a deterministic system is a system in which no randomness is involved in the development of future states of the system.[1] A deterministic model will thus always produce the same output from a given starting condition or initial state
- Non-linear
However, what one person describes as being "non-linear" may not be what someone else does. Similarly, when does a line become not a line? If we say a line as has certain length, height, width or depth, at what point does it not become a line? The same goes for our definition of non-linear, or what is meant by a circle, square, triangle, etc... For example, if we say a triangle has 3 points, can we place the points in positions from which we can not intersect them with lines, such as three points in different dimensions? Is con census amongst others the key to understanding or agreeing what we mean by a given label? If a system does not exhibit a relative straight course over a given length, is it to be called a chaotic, non-linear system, or can a linear system be chaotic as well? Can our numbering system 0,1,2,3,4,5,6,7,8,9 or our alphabet system be exhibits of linear chaotic systems? Just because we artificially assign points of reference which we use to create continuity, does not mean the assigned lineage is not representative of an underlying chaotic system. As such, chaotic systems may very well be able to adopt a camouflaging technique of assumable stability... like a wolf in sheep's clothing. If we can't seem to "connect the dots" of a given system we have given points of reference to, is this automatically to be described as being non-linear, or merely an illustration of our inability to identify points of connection which may act independently and seemingly random? Is a system incoherent, unstable, chaotic, etc., simply because we are unable to pay witness to some intelligibility... because we are using the wrong mental framework for analyzing given perceptions? Just because we look for and assign assumed stability to an otherwise viewed chaotic system such as a society, does not automatically change the chaotic system into a stable one, even when we force and enforce certain elements to suggest a type stability conducive to our sensibilities.
Equations are not only linear, but they are lists of numbers, symbols and orders of operations. If we do not describe an equation as a line... or being a linear arrangement of numbers, symbols, etc., then are we suggesting some other geometrical model? If we say a linear equation is flat... without tone, then do we reserve tones for equations which are circular, triangular or some other geometric form? It is rather silly to describe something as a "system of non-linear equations" instead of saying linear equations describing an assumed non-linear system. As it stands, for example, we can describe three possible types of solutions for points of intersection of a parabola and a line ( Systems of Nonlinear Equations and Inequalities - Two Variables):
- No solution - The line will never intersect the parabola.
- One solution - The line is tangent to the parabola and intersects the parabola at exactly one point.
- Two solutions - The line crosses on the inside of the parabola and intersects the parabola at two points.

As another example, we can also describe three possible solution sets for a system of equations involving a circle and a line:
- No solution - The line does not intersect the circle.
- One solution - The line is tangent to the circle and intersects the circle at exactly one point.
- Two solutions - The line crosses the circle and intersects it at two points.

>Chaos theory is a branch of mathematics focusing on the study of chaos — dynamical systems whose apparently random states of disorder and irregularities are actually governed by underlying patterns and deterministic laws that are highly sensitive to initial conditions. Chaos theory is an interdisciplinary theory stating that, within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnectedness, constant feedback loops, repetition, self-similarity, fractals, and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning that there is sensitive dependence on initial conditions). A metaphor for this behavior is that a butterfly flapping its wings in Texas can cause a hurricane in China.
Small differences in initial conditions, such as those due to errors in measurements or due to rounding errors in numerical computation, can yield widely diverging outcomes for such dynamical systems, rendering long-term prediction of their behavior impossible in general. This can happen even though these systems are deterministic, meaning that their future behavior follows a unique evolution and is fully determined by their initial conditions, with no random elements involved. In other words, the deterministic nature of these systems does not make them predictable. This behavior is known as deterministic chaos, or simply chaos. The theory was summarized by Edward Lorenz: "Chaos: When the present determines the future, but the approximate present does not approximately determine the future.".
Let us not forget that equations are themselves lists and systems of linear expressions. They are lists of numbers and/or symbols and orders-of-operation that sometimes create conditions whereby an individual becomes habituated in how their perceptions are organized. If a perception can be organized mathematically, they may well assume that their perception of a given situation refers to a consistency that they may further interpret as a rule, axiom (assumption/belief) or Natural law. They also tell any eavesdropping extraterrestrials much about human memorization, depth perception, language skills, visual and visualization acuities, and of course, cognitive processing. Vary often there is to be seen pairing and dichotomization like that seen in other subjects, and yet none of the subjects... except for a few philosophers and physicists... if not Biologists and cultural Anthropologists (along with some computer programmers); take into consideration the recurrence of such dichotomization as an expressed recurrence of human cognitive activity as if most people rely on simple serrations of thought processing which follow an A,B,C... 1,2,3 formulation in some manner. Let us also not overlook the "bunching" of multiples to produce a conservation called a solution. In my mind, a linear equation gives the impression of a funnel or triangle turned with the large "mouth" end facing towards the left (for western perspectives) and the fulcrum or exit/anus end pointed in the right-hand direction. Hence, it can be viewed either as a clock-wise or widdershins (counter clock-wise) direction.

Images from:
- How to create a conversion fueled sales funnel by Matthew Davies, 28 Aug, 2019
- How Is Digital Marketing Feeding Your Sales Funnel by Douglus Karr, Sun. Feb. 28, 2021
- How to build a social media marketing funnel that converts by Sarah Aboulhosn, Feb. 19, 2020
To me, funnels and other geometric forms can be viewed as a Mathematical Object, though in the present sense the funnels are being used to describe the overall layout of an equation instead of a single number or set of numbers or variable. However, visualizing a static or non-moving object is one thing (in this case a funnel), it is quite different than visualizing a dynamic or moving funnel which may have intermittent oscillations.
If we compare the funnel idea of mathematical equations to the funnel idea for the creation of the Universe coupled with the notion of mirror-imaging (and the presence of mirror neurons in our brains), the reversibility of equations presents us with an exercise consistent with the idea of equilibrium. We need only provide several scenarios as to the origin of and (supposed) eventual trek for the Universe; we can visualize different variations of equations put into a pictographic model:
The following CONE images are just a few considerations of different scenarios related to the ideas of a Big Bang expansion and Universe collapsing (the assumed Big Crunch). Visually mix and match, flip them over, angle them, as well as distort them as you please:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
3 mem-Brane Cyclic Big Bang Universe? (page 3)
One must ask whether a "cone" idea is appropriate for the development and shape of the Universe as it entered existence and is thought to eventually exit it. While those of the Western mindset are accustomed to portray and look at life through a left-to-right prism, we should nonetheless train ourselves to consider alternative scenarios, though in doing so we are confronted with the usage of three variations involving:
- left-to-right/right-to-left
- up-and-down/down-and-up
- diagonal
These configurations remind me people involved with a board game set of rules like checkers or chess within a confined space of 64 squares which is numerically significant when looking at biology with respect to the quantity of amino acids, from which we can enlist multiple expressions of numerical gymnastics such as: (64 - 3 stop codons and 1 start codon... leaving us with a base 60 or base 20 multiplied 3 times, or a base ten multiplied 6 times or base five multiplied 12 times, etc...). While some mathematicians may discount such an exercise as numerology, it is logical for numerological considerations to be a part of a larger equation so that its value or uselessness can be dismissed but noted as a consideration that they human mind is capable of reviewing... just as an observer might watch children at play but not actually engage in the type of play taking place. The knowledge that children play in given ways is a useful addition to one's overall knowledge just as are alternative considerations of numerological digression. Dismissiveness without consideration is both arrogance and prejudicial, if not egotistical. Hunting for a new type of mathematics to supersede all present forms may or may not exist in mathematics as it is presently being practiced.
Date of Origination: 26 February 2021... 6:59 AM
Initial Posting: 1st July 2021... 4:44 AM