(Static -vrs- Dynamic Equations)
1
~ The Study of Threes ~
http://threesology.org
Visitors as of 2/27/2021

Let me begin by explaining my usage of the word "Accordian" instead of the word spelled as "Accordion". Initially it was a spelling error but later came to be identified as an intellectual 'aside' which merited usefulness. In fact, as I toyed with the word after discovering the error I came to find that the word in which I was using it had a better echo in my mind since I was pronouncing the word with an "an" sound and not an "o" sound. Such a musing further displayed the word with the other vowels (AEIOU-Y): Accordian, Accordien, Accordion, Accordiun, Accordiyn. It made an impact because of my usual penchant for writing poetry with end rhymes. |

Accordion image source |
With respect to rhymes:
- If we use general words to describe the types of rhymes due to a "geographical" (or geometrical) location (and not complicate it by describing each word or each letter as a numerical reference): we can resort to a dichotomy and say there are internal (inside a given line or lines), and external ones (at the beginning or end of a line or lines). Please note I emphasized the word "one" so as to insert a rudimentary mathematical (number/counting) reference.
- However, please note that some people prefer to use the words front and tail or beginning and ending... or some other preference for
identifying the first word and last word rhymes. For example; let us say the rhymes are broken down numerically as 1st, 2nd, 3rd, indicating
first word, some internal word, and last word. Hence, the 1st might be called: head rhyme or initial rhyme. The 2nd might be called internal rhyme.
3rd: tail rhyme. With respect to the usage of the word "Alliteration" as a reference sometimes used to describe a head rhyme, we very often see the repetitive
usage of a vowel and/or consonant such as the frequently cited: She sales sea-shells by the sea-shore (which, incidentally was in reference to the Victorian
fossil hunter Mary Anning. It was originally a song, with words by Terry Sullivan and music by Harry
Gifford, written in 1908, inspired by Mary Anning’s life.
She Sells Seashells and Mary Anning:
Meta-folklore with a Twist by Stephen Winick, July 26, 2017).
- The three-word narrative "location- location- location" is frequently applied to real estate contexts, but is sometimes appropriated for other business contexts as well as being used by some detectives citing it as a necessary element when solving a crime. Yet, it can be used in the context of any subject such as the necessity of placement for variables in the "territory" of a mathematical equation... as well as words in a sentence, or sentence in a paragraph, or chapter in a book or book in a series, etc...
- Again... using words, we can and also reference three types of rhyme "location" by describing beginning, middle, and end rhymes occurring within a single (one) sentence or two or more sentences (lines). Please note that the repeated usage of the word "lines" is intended to invoke the imagery of more involved geometrical imagery to be visualized.
- The presence or absence of rhymes in a given (numerically related) order, can also act as a visual cue for the usage of a cipher using either a 3-item "dot-dash-dot" Morse code regimentation, or a 2-line 6-item configuration that may or may not also utilize the flag-waving semaphore form of speech so as to display that an emphasize is being directed towards a line-of-sight preference over an auditory one, thus shifting to another type of rhyme using a different perceptual sense.
- While one can also resort to the typical referencing of rhymes using letters from the alphabet such as the rhyme schemes of ABAB, AABB, AAAB, AAAA, (and BBBB, etc... (when internal rhymes are used synchronously)— or otherwise without resorting to a substitution with numerical values (1212, 1122, 1112, 1111); more complicated rhyme patterns are not typically used in a general sense by most poetry writers, and require a rule-of-thumb or (a kind of map-) "legend" if a writer wishes readers to traverse such a landscape with any intelligibility or attempted mathematically oriented survey.
- In other words, readers must be told what unorthodox method is being used and why it is... though in doing so, those readers with expectations of reading a poem may mean that they expect it to have certain values which they favor. The same goes for writing on any topic.
- Numerically speaking, there are specifically named mono-rhymes, Couplet-rhymes (dual), triple-rhymes (also Terza rima), quatrains, quintuplets, sestains (also sestet), but thereafter the numerical referencing is particularly sparse. While a given person can use a specific number of lines over and over as a type of personal signature, it must be noted that they types of rhyme schemes is limited, even when you include combinations and "free-styles". This realization is an important identity in the overall conversation about rhyme schemes because it speaks to the consideration which should be given when the topic of cognitive limits is discussed... as is quite evident in mathematics, since the language and equations being used follow "rhyming" patterns as well. You just need to have them pointed out to be cognizant thereof... in other words, routine repetitions are being used.
- One last reference for "rhyming" should be noted in the sense of acknowledging a repetition. Repetitions come in many forms. The image below displays an example of what I call "sight" rhyme, where observed repetition can be construed to represent an act of rhyming.
- This link may be of interest for some readers: Rhyme scheme, even though it is pretty basic.

Altering the type of rhyme according to how one is pronouncing a word can produce unforeseen combinations not only of words, but of preceding thoughts about the content of the line and those that follow. So true is this with Mathematic's. You can change one number, one sequence, one variable, one interpretation, and have a different statement... even though you may force yourself into complying with some rule-of-thumb like an autistic who must do things in a certain way in a certain order within a certain time frame. While this is a disposition an accountant might hold near and dear to their perspective of reality (or they might well be fired... unless specifically hired to perform "creative accounting"), those seeking the trails of Pure Mathematic's are not so encumbered... unless they suffer from playing follow my/the leader too much. In a sense they are those who strive to indulge in conversations with their creative muse whose content is so engrossing that once they look up, they may find themselves in unfamiliar territory (either scared or enthusiastic). Likewise, I too choose this exploratory route of getting lost in order to discover the possibility of the new. So engrossed were (and are) some people in their work that they adopted life styles that many of us would view as odd, strange, eccentric or even exhibiting a touch of madness.
In present views of positive psychology, a flow state, also known colloquially as "being in the zone", is the mental state in which a person performing some activity is fully immersed in a feeling of energized focus, full involvement, and enjoyment in the process of the activity. In essence, flow is characterized by the complete absorption in what one does, and a resulting transformation in one's sense of time. Yet, like many views in psychology that do not themselves experience an actual "flow state" in the sense of immersing themselves philosophically deep enough to acquire a larger perspective of the idea being presented, or the description used to illustrate the idea of a flow would thus also realize that if a person is able to acknowledge they are in a "zone" (or landscape, territory, domain, etc...), then they cannot be too deep. Recognition of being in a 'zone' means that the energy being used for such an acknowledgement is a proportion of the total available energy being wasted... (like a vehicle's engine where most of the heat energy is lost to the environment and cannot be utilized because of the wasteful energy design); unless of course one would want to suggest that such a state of recognition requires a small amount of energy because the human mind or mental activity is a waste-small or waste-free energy utilizing activity/mechanism. If the amount of energy is small then the usage of a "self-regard" observational diversion is negligible, but if it is large, then a person is not necessarily so very deep in a 'zonal domain' which they are otherwise capable of achieving a greater focus of effort and ultimate expression of gain.
H.O.B. recapitulation note: A total emersion of "being in the zone" and being able to recognize that one is experiencing what one believes to be a "zone" are not necessarily the same states of experience... or even levels of consciousness... and has an exploratory application when speaking about mathematical orientations in particular. Indeed, there appears to be a sequential activity we might describe as a position before, in-the-zone, and after the occurrence... Which is not a remarkable realization since many events have the same sequence to be referenced, yet in this case we acknowledge that "being in the zone" is not necessarily a singular pointed event which takes place like some sort of Eureka! encapsulation of spontaneity... but takes place progressively, unless there are those who can jump, or step "into" a zone, instead of swimming, dancing, and otherwise moving along a 'jumping onto squares' (like a child playing hopscotch) or playing some measure of leap frog from one level of mental activity to another (or perhaps in a retrogressive conscious fashion leading onto a landscape that other have difficulty reaching the same levels or heights of).
While it is not difficult to consider that a "zone" may be viewed s a personalized expression of experience, wisdom, intuition, creativity, talent, if not luck and even genius... unless such an idea is only true to the extent we have different types of zone needed for different types of activities (whereby others can experience the same or very similar type of zone) or that the type of zone in a particularized activity also reflects an individualized reference of personality and "dimensional shift of mental presence" one is enabled to enter into. In other words, a person's "zone" is equal to the level in which they will exhibit mediocrity, aptitude, talent, creativity or genius. For example, when Newton, Davinci, Einstein, etc., enter their particular "zones" of contemplation or "distraction", it is different from the zone in which a non-genius enters into... and the same goes for their oddness or eccentricity, however a particular behavior is labeled.
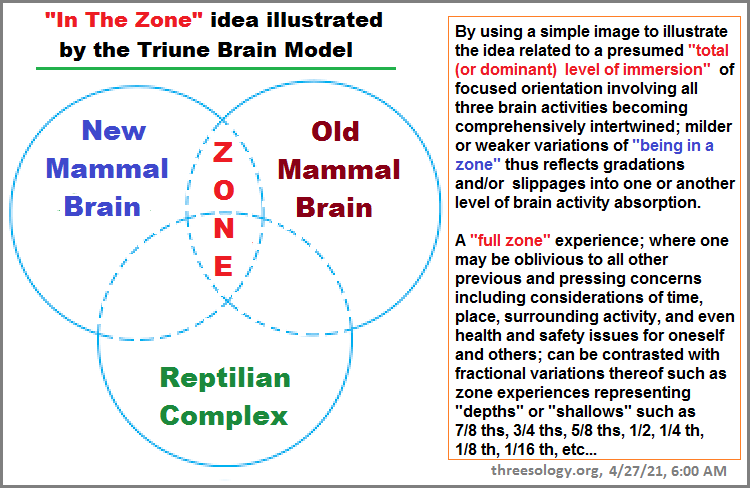
Let's put this another way, while at the same time referencing the "zone" in the present context of discussion directed towards mathematics; such that "being in the zone" might well entail a description of how involved a person is in a given task of solving or creating an equation. It would appear that the model of a 3-stage immersion scale of measurement will suffice to provide an explanation, though someone might want to add additional interstitial stages before, during, or after such as a pre- and post-before, pre- and post-during and pre- and post after... because the words "before, during, after" are insufficiently equipped to provide details. If we turn to the usage of numbers, we might use 1, 2, 3, with or without resorting to fractions, decimals and square roots to provide infinitesimal fractionations in an attempt to be more precise and inclusive. Yet, generally speaking, to be aware of beginning to get into a "zone" (equation) and being aware that one is in a frame of mind that a person describes as a zone, (equation) is wholly different from a person being what we believe to be exclusively immersed in a zone (equation) where they are actually oblivious to being in a zone (performing an equation). For example, during a writing task when all the students in my 3rd grade class were told to sit up straight and engage in a given task of writing, when I looked up after having finished, everyone was looking at me and the teacher was standing over me saying that she had been poking me quite hard with her (instructor's wooden stick), but I had felt nothing. In short, I do know one measure of the so-called "zone".
If one takes, for example, the model of the Triune brain developed by Paul D. MacLean as an analogy to the idea of 3 zones a mathematician (or anyone in any activity) may experience, the 1st zone can be view as being revealed by the idea of a primitive brain called the Reptilian Complex. This can serve as a representative example of simplistic mental activity like the routine mechanics of many equations. Typically, most people are fully aware of their participation in such an exercise... from which they can be easily diverted to do some other task. In other words, the depth of this "zone" is quite shallow or quite distant from higher mental functioning, though it was born in the deepest part of the past (in evolutionary terms).
The 2nd zone, equated with the Limbic System (Paleo-mammalian Complex), can be equated with mathematical activities involving a higher form of mathematical activity, yet even in such exertions the person(s) involved may switch momentarily back and forth from greater to lesser depths of immersion in their problem solving efforts. For example, they may stop for a break, or get something to eat, or run an errand, lose time, forget to do some expected activity, etc... The depth of this zone's development in evolutionary terms lays between the 1st and 2nd zones, and therefore can be said to be a person with one foot facing forward and one foot facing backward.
Whereas the 3rd zone, equated with the New Cortex (Neo-mammalian Complex), that some claim is reserved for those involved with mathematical equations and other maths activities which can not be interrupted and that those involved may indeed "zone out" any interference in order to accomplish a give task at hand; may otherwise be viewed as a person to be called a "space case", or "living in their own world", or "out of touch with reality". However, so long as they are involved in a task within an environment that fully recognizes their "zoned-in/ zoned-out" behavior as a particular mindset typically occurring within a given provenance of activity, their other-wise labeled "eccentricity of mind" is socially acceptable... and typically not seen by the "average" public because it occurs under the auspices of protection given by an institution of declared higher learning which fully recognizes such behavior as a natural and normal component which enables a person to mentally exercise in a realm... in a dimension... in a domain most conducive for a person to pursue their trail-blazing activities.
While there are some who do not like the idea of a triune brain model (for example: You Don't Have a Lizard Brain by Daniel Toker),
I bring up the aforementioned topic of oddness as a type of caveat when introducing the idea of a dynamic equation requiring its own set of axioms and proofing mechanisms which need to be developed by a reexamination of multiple forms of data from all subjects. We can not design a new model of mathematics without developing new assumptions, beliefs and their following axioms... out of which the validation of proofs can emerge to suit the... let us say either— "enlightened purposes"... or if not simply 'additional' formulations; though starting with the uses of traditional proofs can be useful as a warm-up. Hence, lots of information has to be interviewed and illustrated so as to point out a new realization to act as revelation embodying an insight which has not been actualized, though multiple readers may well have entertained such perceptions themselves in different contexts and made use of them for different applications.
One of these re-examinations is to look about nature and take stock of trees. Yes, trees... since not only can trees be used as a metaphor for varying ideas to be illustrated with the notions of root, roots, rootedness, branch, branching, branches, foliage, (circularly displayed) ring growth, symbiosis (with a given environment and insects/animals), etc... However, since I will elaborate further on this later, let me merely mention that there is a linear, circular, and triangular pattern which stares us in the face, but such a pattern has not been recognized to the extent of being part of any present day teaching curriculum.
In other words, you won't find such a growth pattern being illustrated in common nor uncommon text books. Like ancient mathematicians who were naive about the existence of Algebra, Trigonometry, Calculus, etc., and Astronomers were naive about physics, present day Horticulturalists are naive about a very simple observation to be made. In fact, multiple people may argue against such a view but this is the usual story when new ideas are presented about information which everyone has access to, but simply overlooked the realization. However, the growth pattern of trees exhibiting a linear, circular, triangular conformation is but one of several examples. Another is seen in the design of the internal combustion engine, even though different words may be used to describe these three geometric forms. For example, we have:
- Linear (in-line, horizontally opposed, slanted) engines.
- Circular engines such as seen in the old aircraft models.
- Triangular engines such as the v-shaped model, though one might argue for the inclusion of the rotary engine as well>.
Another example of the linear, circular, triangular representation might be said to be seen in the flight patterns of birds:
- Linear (singular as seen in some migration patterns or sometimes broad lines of linear exhibition such as in Starling murmerations).
- Circular (bunched up groupings).
- Triangular (commonly referred to as V- or Vee-shaped migrating flight patterns).
The presence of multiple examples of the linear, circular, triangular configurations as an ensemble (the Pythagorean theorem of A2 + B 2 = C2 is a well known three-patterned ensemble); provides a precedent when we examine the structure of mathematics as an expression of cognitive activity. In other words, we have linear equations but no circular and triangular ones. We have linear equations which express circular and triangular forms, but no circular and triangular equations expressing any of the others. I am suggesting that if the linear- circular- triangular configuration is a common theme of expression of human thinking as seen in multiple other activities, then the absence of the circular and triangular forms configured as "stand-alone" models set next to the common linear forms, suggests a number of reasons. One of which is that the human brain has not yet evolved enough. Another is that the present practice of mathematics is too primitive for such configurations to evolve out of as one might suppose to be a developmental trend. A third possibility is that the linear form of equation has been so firmly embedded into cultural practices we take it as a given... as natural as flowing water, or falling rain, or blowing winds, or tides, etc... Then again we may not create circular and triangular equations... that is, dynamic equations, simply because the idea as not come to our mind, just as simple arithmetic did not come to the minds of those in the deep past who were learning to count.
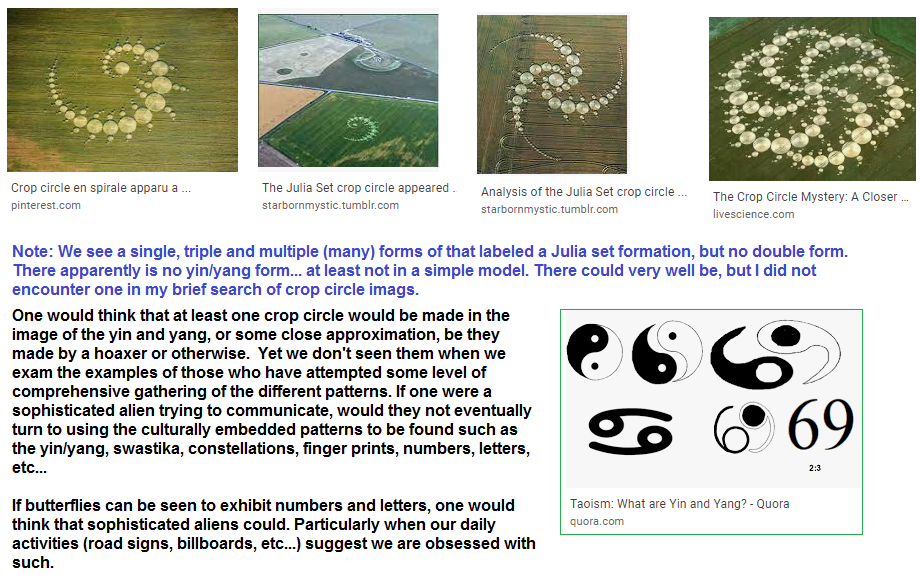
Here are a few images of different flight patterns of Starlings captured from a Google images internet search using the term "Murmuration". Incidentally, We might want to label these as Starling "formations" akin to crop circle formations, though both of which might be said to exhibit a "message" that many people, similarly, interpret to be an honest means of labeling the Nazca lines of Peru. However, neither the Murmurations of Starlings, the Crop Circles, nor the Nasca lines have been subjected to an interrelated mathematical investigation. An artistic one yes, but any attempted mathematical interpretation might well influence one to think in terms of an artistic venture an apply some sort of Fractal labeling so as to hint of a mathematical inquiry instead of a dominant artistic inclination, whereby the usage of the term "fractal" is somehow supposed to lend an artistic inclination with a higher level of sophistication.


The Butterfly Alphabet is a photographic artwork by the Norwegian naturalist Kjell Bloch Sandved. Sandved worked at the Smithsonian's National Museum of Natural History in Washington, D.C., and came up with the idea with Barbara Bedette, a paleontologist, of finding all 26 letters of the Latin alphabet and the Arabic numerals 0 to 9 in the patterns on the wings of butterflies. Sandved's photographic excursions led him to Brazil, Congo, Papua New Guinea and the Philippines. Searching for the forms took him over 24 years, but he finished the collection in 1975 and published it in the Smithsonian Magazine. It was republished by Scholastic as a book in 1996, with accompanying snippets about butterfly species. Butterfly Alphabet |
Photographs can be used to provide proof, but introducing an equation as if it were a Natural photograph of one's thinking or a characteristic of the human mind in a super-normal state; requires a bit more proof than mere "squiggles" on a page as one who is unfamiliar with mathematics might label an equation. However, a short paragraph about proofing is wholly insufficient for addressing what is seen as impoverization of mathematical instruction in pre-college courses which leads to students in later education pursuits faced with the problem of having to learn how to think in terms of proofing their work... either after something is accomplished like that which occurs when other scientists executed the same methods and manners of someone's claim(s) so as to determine whether or not the result is verifiable by recurring repetitions by others; or during the course of a task such as a plumber and electrician do when testing a circuit or whether or not a plumbing joint will leak. Because proofing is such an important criteria for mathematicians as well as building trades and mechanical/plumbing/electrical aptitudes when working on a vehicle; the issue for the rather stark absence of such training is an effort some have taken up, to remedy, such as is discussed here: Proof as a Tool for Learning Mathematics by Eric J. Knuth.
However, when we deal with a large variety of data that has not yet been "translated" into a readily comprehensible list of variables to be placed into an equation... a type of equation that most may not have even heard of, where does one start? No less, will the old (and entrenched young) dogs of mathematics be able to learn new tricks of thinking? Much like the later born generations of mathematical students in decades past who looked at the once non-mathematically oriented subjects and began applying mathematics to the data, how will they be able to see a "new math" if they are like those of old who have long become accustomed to their particular usage of mathematics? Will they be as a chimpanzee who is comfortable using a twig to fetch out a tidy insect morsel, but be lost when confronted with one or more tools that in the hands of another yield more than just a single insect? Like giving a skilled abacus user a calculator who looks at it, plays with a while and then tosses it aside for the more familiar... no doubt such a reaction is to be expected.
No less is the case for when they may be confronted with a new proofing methodology within criteria they are appreciably unaware of. Alas, we can lead a horse to water, but we can not make it drink. We can direct someone to get out of a lightning storm, but if they think they are somehow unlikely to get struck, because they enjoy the fall of rain so much after a long drought; what can one do but hope they will be lucky enough not to have to experience the changes if a deluge is about to happen. (Take the comment as you will.) Hence, in short, along with a new type of equation is the need for a new type of proofing ideology as well as Axioms rendered from different assumptions and beliefs when a larger array of information is presented. The development of our standard proofing system can be represented with a short excerpt:
 Transcript: The Language of the Universe The Story of Maths by Marcus du Sautoy Youtube presentation: BBC. The Story of Maths. The Language of the Universe Wikipedia article on author: Marcus du Sautoy |
Transcript excerpt:
Just like the Babylonians before them, the Greeks were passionate about mathematics. The Greeks were clever colonists. They took the best from the civilizations they invaded to advance their own power and influence, but they were soon making contributions themselves. In my opinion, their greatest innovation was to do with a shift in the mind.What they initiated would influence humanity for centuries. They gave us the power of proof.Somehow they decided that they had to have a deductive system for their mathematics and the typical deductive system:
It's the power of proof which means that the discoveries of the Greeks are as true today as they were 2,000 years ago. |
Without such an introductory caveat, a reader may not be as receptive, may not be as open-minded to the idea of a new model of mathematics emerging from an innocence in crude surroundings, just as many people rejected the in-a-manger beginnings of Christianity, or the desert dwelling beginnings of Islam, or any of the other unlikely seeming spots (and people involved) in the origination for many ideas,. particularly if they are expecting a Dynamic equation to look like those equations a given reader is accustomed to; in line with multiple perceptions of a reality which they are immersed in, but may well take for granted or be dismissive of as having little mathematical relevance with respect to expected mathematical symbology. Indeed, let me ask a question that will be asked later on: How is a person to know what a Dynamic equation is to look like if they are expecting something to be illustrated in a manner that they are accustomed to viewing an equation? Similarly, in what form would you expect an Extra-terrestrial to be in and what knowledge do you expect them to have... and what if it is nothing like any human interest... including mathematics, language or other convention? A math equation appearing in a 1-dimensional form is different from a 2-dimensional form which is also different from a 3-dimensional form. In more everyday terms, it is like comparing Islam to Buddhism or polytheism to monotheism. If you have been entrenched in the culture of one subject such as mathematics for so long that you have come to embrace it as the one and only means of reaching a desired standard of truth; presenting you with an idea that may well appear to be foreign, or even odd, needs some measure of preparation so as to avert the possibility of automatic rejection because you don't see a given flag being waved in a certain way accompanied by a given musical chorus.
Date of Origination: 26 February 2021... 6:59 AM
Initial Posting: June 2nd, 2021...3:42 AM